7.1. 外積の定義
3 つの非同一平面上にあるベクトル a 、 b 、 c は、示された順序で取得され、3 番目のベクトル c の終端から最初のベクトル a から 2 番目のベクトル b への最短回転が反時計回りであるとみなされる場合、右トリプルを形成します。時計回りの場合は左になります (図 16 を参照)。
ベクトル a とベクトル b のベクトル積はベクトル c と呼ばれ、次のようになります。
1. ベクトル a および b に垂直、つまり c ^ a および c ^ b;
2. これは、ベクトル a とベクトルに基づいて構築される平行四辺形の面積に数値的に等しい長さを持ちます。b側面のように（図17を参照）、つまり
3. ベクトル a 、 b 、 c は右トリプルを形成します。
ベクトル積 a x b または [a,b] で表されます。 ベクトル積の定義から、オルト間の次の関係が直接続きます。 jと k(図 18 を参照):
i x j \u003d k、j x k \u003d i、k x i \u003d j。
たとえば、次のことを証明してみましょう私はxj \u003d k。
1) k ^ i , k ^ j;
2) |k |=1 ですが | i×j| = |i | |J| sin(90°)=1;
3) ベクトル i 、 j および k右トリプルを形成します (図 16 を参照)。
7.2. 外積特性
1. 因子を並べ替えると、ベクトル積の符号が変わります。 およびxb \u003d（b xa）（図19を参照）。
ベクトル a xb と b xa は同一直線上にあり、同じモジュールを持ちます (平行四辺形の面積は変化しません) が、反対方向を向いています (トリプル a、b、a xb および a、b、b x a は反対向きです)。 あれは アクサ = -(bxa).
2. ベクトル積には、スカラー因子に関する組み合わせプロパティがあります。つまり、l (a xb) \u003d (l a) x b \u003d a x (l b)。
l >0 とします。 ベクトル l (a xb) はベクトル a とベクトル b に垂直です。 ベクトル ( 私 a) × bはベクトル a およびベクトルにも垂直です b(ベクトル a, 私ただし、同じ平面上にあります）。 したがって、ベクトルは 私(xb) と ( 私 a) × b共線的。 両者の方向が一致していることは明らかです。 それらは同じ長さです:
それが理由です 私(a xb)= 私 xb。 についても同様に証明される 私<0.
3. 2 つの非ゼロベクトル a と bそれらのベクトル積がゼロ ベクトルに等しい場合にのみ共線的になります。つまり、||b<=>そしてxb \u003d 0。
特に、 i *i =j *j =k *k =0 です。
4. ベクトル積には分布特性があります。
(a+b) xs = a xs + b xs 。
証拠なしで受け入れます。
7.3. 座標に関する外積表現
ベクトル外積テーブル i を使用します。 jそしてk：
最初のベクトルから 2 番目のベクトルへの最短経路の方向が矢印の方向と一致する場合、その積は 3 番目のベクトルと等しくなります。一致しない場合、3 番目のベクトルにはマイナス符号が付けられます。
2 つのベクトルを a =a x i +a y とします。 j+az kそしてb=bx 私+by j+bz k。 これらのベクトルを多項式として乗算して、これらのベクトルのベクトル積を求めてみましょう (ベクトル積の特性に従って)。
結果の式はさらに短く書くことができます。
等式 (7.1) の右辺は、最初の行の要素に関する 3 次行列式の展開に対応するため、等式 (7.2) は覚えやすいです。
7.4. 外積のいくつかの応用例
ベクトルの共線性の確立
平行四辺形と三角形の面積を求める
ベクトルの外積の定義によると あそしてb |a xb | =| ある | * |b |sing 、つまり S par = |a x b |。 したがって、DS \u003d 1/2 | a x b |。
点の周りの力のモーメントを決定する
点Aに力を加えてみます F =AB手放す だいたい- 空間内のどこかの点 (図 20 を参照)。
物理学から知られているのは、 トルク F 点に対して だいたいベクトルと呼ばれる Ｍさん、点を通過するもの だいたいと：
1) 点を通る平面に垂直 O、A、B;
2) 数値的には力と肩の積に等しい
3) ベクトル OA と A B で右トリプルを形成します。
したがって、M \u003d OA x F。
回転の線速度を求める
スピード v角速度で回転する剛体の点 M w固定軸の周りの値は、オイラーの公式 v \u003d w x r、ここで r \u003d OM、O は軸の固定点です (図 21 を参照) によって決定されます。
意味。 ベクトル a (乗数) と、それと同一直線上にないベクトル (乗数) とのベクトル積は、3 番目のベクトル c (積) であり、次のように構築されます。
1) その係数は、数値的には図の平行四辺形の面積に等しい。 155)、ベクトルに基づいて構築されます。つまり、前述の平行四辺形の平面に垂直な方向に等しいです。
3) この場合、ベクトル c の方向は、ベクトル c が右手系を形成するように (2 つの可能な方向から) 選択されます (§ 110)。
指定: または
定義への追加。 ベクトルが同一線上にある場合、その図形を (条件付きで) 平行四辺形とみなして、ゼロ面積を割り当てるのが自然です。 したがって、共線ベクトルのベクトル積はヌル ベクトルに等しいと見なされます。
ヌル ベクトルには任意の方向を割り当てることができるため、この規則は定義の項目 2 および 3 と矛盾しません。
備考 1. 「ベクトル積」という用語の最初の単語は、アクションの結果がベクトルであることを示します (スカラー積とは対照的です。§ 104、備考 1 を参照)。
例 1. 正しい座標系の主ベクトルのベクトル積を求めます (図 156)。
1. 主ベクトルの長さはスケール単位に等しいため、平行四辺形 (正方形) の面積は数値的には 1 に等しくなります。 したがって、ベクトル積の係数は 1 に等しくなります。
2. 平面に対する垂線が軸であるため、目的のベクトル積はベクトル k と同一直線上にあるベクトルになります。 そして、両方の法が 1 であるため、必要な外積は k または -k のいずれかになります。
3. ベクトル k が右側のシステムを形成する (およびベクトルが左側のシステムを形成する) ため、これら 2 つの可能なベクトルのうち、最初のベクトルを選択する必要があります。
例 2. 外積を求める
解決。 例 1 と同様に、ベクトルは k または -k であると結論付けます。 しかし、ベクトルは右側のシステムを形成する (ベクトルは左側のシステムを形成する) ため、ここでは -k を選択する必要があります。 それで、
例 3 ベクトルの長さはそれぞれ 80 cm と 50 cm で、角度は 30° です。 メートルを長さの単位として、ベクトル積 a の長さを求めます。
解決。 ベクトル上に構築された平行四辺形の面積は次のとおりです。 目的のベクトルの積の長さは次のとおりです。
例 4. 長さの単位としてセンチメートルを使用して、同じベクトルの外積の長さを求めます。
解決。 ベクトル上に構築された平行四辺形の面積はベクトルの積の長さに等しいため、2000 cm、つまり
例 3 と 4 を比較すると、ベクトルの長さは因子の長さだけでなく、長さ単位の選択にも依存することがわかります。
ベクトル積の物理的な意味。ベクトル積で表される多くの物理量のうち、力のモーメントのみを考慮します。
力の作用点を A とすると、点 O に対する力のモーメントはベクトル積と呼ばれます、このベクトル積のモジュールは数値的には平行四辺形の面積に等しいため (図 157)、モーメントのモジュールは、底面と高さの積、つまり、力に点 O から力が作用する直線までの距離を掛けたものに等しくなります。
力学では、剛体の平衡には、物体に加えられる力を表すベクトルの合計だけでなく、力のモーメントの合計もゼロに等しくなる必要があることが証明されています。 すべての力が同じ平面に平行である場合、モーメントを表すベクトルの加算は、それらの係数の加算および減算によって置き換えることができます。 しかし、力の任意の方向については、そのような置き換えは不可能です。 これに従って、外積は数値としてではなくベクトルとして正確に定義されます。
意味。 ベクトル a とベクトル b のベクトル積は、記号 [«, b] (または l x b) で示されるベクトルです。1) ベクトル [a, b] の長さは (p、ここで y はベクトル a と b の間の角度 (31); 2) ベクトル [a, b) はベクトル a と b に垂直です。 これらのベクトルの平面に垂直。 3) ベクトル [a, b] は、このベクトルの端から a から b への最短回転が反時計回りに発生するように方向付けられます (図 32)。 米。 32 Fig.31 言い換えると、ベクトル a、b および [а, b) はベクトルの右トリプルを形成します。 右手の親指、人差し指、中指のような位置にあります。 ベクトル a と b が同一線上にある場合、[a, b] = 0 であると仮定します。定義により、ベクトルの積の長さは、乗算されたベクトルに基づいて構築される平行四辺形 (図 33) の面積 Sa に数値的に等しくなります。 a と b は側面と同じです: 6.1 。 ベクトル積のプロパティ 1. ベクトル積は、乗算されたベクトルの少なくとも 1 つがゼロである場合、またはこれらのベクトルが同一線上にある場合 (ベクトル a と b が同一線上にある場合、それらの間の角度) に限り、ゼロ ベクトルと等しくなります。は 0 または 7r のいずれかです)。 これは、任意のベクトルに対するゼロ ベクトルの共線を考慮すると、ベクトル a と b の共線性の条件は次のように表すことができるという事実から簡単に得られます。 2. ベクトル積は反可換です、つまり、常にです。 実際、ベクトル (a、b) と は同じ長さを持ち、同一線上にあります。 これらのベクトルの方向は反対です。ベクトル [a, b] の端からは a から b への最短回転が反時計回りに発生し、ベクトル [b, a] の端からは時計回りに発生することがわかります (図 1)。 34）。 3. ベクトル積は加算に関して分配的性質を持ちます。 4. 数値因数 A はベクトル積 6.2 の符号から取り出すことができます。 座標で与えられるベクトルのベクトル積 ベクトル a と b が基底の座標で与えられるとします。 ベクトル積の分布特性を使用して、座標で指定されたベクトルのベクトル積を求めます。 混合作業。 座標 ort のベクトル積を書き出してみましょう (図 35): したがって、ベクトル a と b のベクトル積について、式 (3) から、1 行目の要素に関する次の式行列式を取得します。 4)。 例。 1. ベクトルに基づいて構築された平行四辺形の面積を求めます 三角形の面積を求めます(図36)。 三角形JSCの面積b "dが、平行四辺形O AC Bの面積Sの半分に等しいことは明らかです。ベクトル積（ベクトルa \u003d OAとb \u003d b \u003d obのベクトル積（a, b |）を計算します） ), (a, b), c) = [a, |b, c)) は一般の場合には当てはまりません. たとえば、a = ss j の場合、§ 7. ベクトルの混合積を得ることができます。 3 つのベクトル a、b、c。ベクトル a と 1> をベクトル的に乗算します。その結果、ベクトル [a, 1>] が得られます。それにベクトル c をスカラー的に乗算します: (k b), c。数値 ( [a, b], e) はベクトル a, b. c の混合積と呼ばれ、記号 (a, 1), e) で表されます 7.1. 混合積の幾何学的意味ベクトル a、b、および一般点 O からのベクトル (図 37)。4 つの点 O、A、B、C がすべて同じ平面内にある場合 (この場合、ベクトル a、b、c は同一平面上と呼ばれます)、混合されたproduct ([a, b], c) = 0。これは、ベクトル [a, b| がベクトル a と 1 が存在する平面に垂直である」という事実、つまりベクトル c であるという事実から導き出されます。点 O、A、B、C が同じ平面上にない場合 (ベクトル a、b、c は同一平面上にありません)、エッジ OA、OB、OS 上に平行六面体を構築します (図 1)。 38a)。 外積の定義により、(a,b) = So c となります。ここで、So は平行四辺形 OADB の面積、c はベクトル a と b に垂直な単位ベクトルであり、三重 a 、b、c は正しい、つまり ベクトル a、b、c はそれぞれ右手の親指、人差し指、中指に位置します (図 38 b)。 右スカラーの最後の等式の両方の部分にベクトル c を乗算すると、座標で指定されたベクトルのベクトル積が得られます。 混合作業。 数値 rc c は、構築された平行六面体の高さ h に等しく、ベクトル c とベクトル c の間の角度が鋭角 (トリプル a、b、c が正しい) の場合は「+」記号を付け、記号「」を付けます。角度が鈍角の場合 (トリプル a、b、c - 左)、したがって、ベクトル a、b、c の混合積は、エッジ上と同様にこれらのベクトル上に構築される直方体の体積 V に等しくなります。トリプル a、b、c が右の場合は -V、トリプル a、b、c - 左の場合は -V。 混合積の幾何学的意味に基づいて、同じベクトル a、b、c を他の順序で乗算すると、常に +7 または -K が得られると結論付けることができます。 プロの図のサイン。 38 参照は、乗算されたベクトルが右または左のどちらのトリプレットを形成するかにのみ依存します。 ベクトル a、b、c が正しいトリプルを形成する場合、トリプル b、c、a および c、a、b も正しいものになります。 同時に、3 つの三つすべて b、a、c; a、c、b、および c、b、a - 左。 したがって、 (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , A)。 乗算されたベクトル a、b、c が同一平面上にある場合にのみ、ベクトルの混合積がゼロに等しいことをもう一度強調します。 (a、b、c は同一平面内です) 7.2. 座標の混合積 ベクトル a、b、c が基底 i、j、k の座標によって与えられるとします: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23)。 それらの混合積 (a、b、c) の式を見つけてみましょう。 基底 i、J、k の座標によって与えられるベクトルの混合積があり、これは 3 次行列式に等しく、その線はそれぞれ、乗算された行列の 1 番目、2 番目、3 番目の座標で構成されます。ベクトル。 ベクトル a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) の同一性のための必要十分条件は、次の形式で書くことができます。 z、ar2 y2 -2 =0。 ウズの例。 ベクトル v = (7,4,6)、b = (2, 1,1)、c = (19, II, 17) が同一平面上にあるかどうかを確認します。 考慮中のベクトルは、行列式がゼロに等しいかどうかに応じて、同一平面上または非同一平面上になります。これを最初の行の要素に関して展開すると、次のようになります。 7.3. 二重外積 二重外積 [a, [b, c]] は、ベクトル a と [b, c] に垂直なベクトルです。 したがって、ベクトル b とベクトル c の平面内にあり、これらのベクトル内で展開できます。 式 [a, [!>, c]] = b(a, e) - c(a, b) が有効であることがわかります。 演習 1. 3 つのベクトル AB = c, W? = o と CA = b は三角形の辺として機能します。 三角形の中央値 AM、DN、CP に一致するベクトルを a、b、c で表します。 2. ベクトル p + q がそれらの間の角度を半分に分割するには、ベクトル p と q の間にどのような条件を接続する必要がありますか? 3 つのベクトルはすべて共通の原点に関連していると想定されます。 3. |p| であることがわかっている場合、ベクトル a = 5p + 2q および b = p - 3q に基づいて構築される平行四辺形の対角線の長さを計算します。 = 2v/2、|q| = 3 H-(p7ci) = f。 4. 共通の頂点から出た菱形の辺を a と b で表し、菱形の対角線が互いに垂直であることを証明します。 5. ベクトル a = 4i + 7j + 3k と b = 31 - 5j + k の内積を計算します。 6. ベクトル a = (6, 7, -6) に平行な単位ベクトル a0 を求めます。 7. ベクトル a = l+ j- kHa ベクトル b = 21 - j - 3k の射影を求めます。 8. A (-4.0.4)、B (-1.6.7)、C (1.10.9) の場合、ベクトル IS "w の間の角度の余弦を求めます。 9. ベクトル a = (3, 6, 8) と x 軸に同時に垂直な単位ベクトル p° を見つけます。 10. ベクトル a = 2i+J-k、b=i-3j + k を辺と同様に構築した平行面の対角線間の角度の正弦を計算します。 ベクトル a と I に基づいて構築された平行六面体の高さ h を計算します (ベクトル a と I に基づいて構築された平行四辺形を底辺とした場合、ベクトル a = 31 + 2j - 5k、b = i-j + 4knc = i-3j + k)。 答え
このレッスンでは、ベクトルを使用したさらに 2 つの演算を見ていきます。 ベクトルの外積と ベクトルの混合積 (必要な方はすぐにリンクを貼ってください)。 大丈夫、完全な幸福のために、さらに、 ベクトルの内積、ますます必要になります。 これがベクトル依存症です。 解析幾何学のジャングルに入り込んでいるような印象を受ける人もいるかもしれない。 これは間違っています。 高等数学のこのセクションでは、おそらくピノキオには十分な薪を除いて、一般的に薪はほとんどありません。 実際、この材料は非常に一般的でシンプルであり、同じものより難しいことはほとんどありません。 スカラー積、さらに典型的なタスクが減ります。 解析幾何学で重要なことは、多くの人が目にしたり、すでに目にしたことがあるように、計算を間違えないことです。 呪文のように繰り返せば幸せになれます =)
ベクトルがどこか遠くで輝いていても 地平線上の稲妻のように それは問題ではない レッスンから始めてください ダミー用のベクトルベクターに関する基本的な知識を回復または再取得します。 より準備ができている読者は、選択的に情報を知ることができるように、実際の仕事でよく見られる最も完全な例のコレクションを集めようとしました
何があなたを幸せにしてくれるでしょうか？ 幼い頃は、ボールを 2 つ、さらには 3 つジャグリングすることができました。 うまくいきました。 これから検討するので、ジャグリングする必要はまったくありません。 空間ベクトルのみ、2 つの座標を持つ平面ベクトルは除外されます。 なぜ？ これがこれらのアクションが生まれた方法です。ベクトルとベクトルの混合積が定義され、3 次元空間で動作します。 もう簡単になりました！
この演算では、スカラー積の場合と同様に、 2つのベクトル。 朽ちない文字にしましょう。
アクション自体が 示される次の方法で: 。 他にもオプションがありますが、私はベクトルの外積を角かっこと十字で囲んで指定することに慣れています。
そしてすぐに 質問: の場合 ベクトルの内積 2 つのベクトルが関係しており、ここでも 2 つのベクトルが乗算されます。 違いはなんですか? まず第一に、結果における明らかな違いは次のとおりです。
ベクトルのスカラー積の結果は数値になります。
ベクトルの外積の結果は VECTOR です。: つまり、ベクトルを乗算してベクトルを再度取得します。 閉店したクラブ。 実際、それがこの操作の名前です。 さまざまな教育文献では、その名称も異なる場合がありますが、ここでは という文字を使用します。
最初に画像付きの定義があり、次にコメントが表示されます。
意味: 外積 非共線的ベクトル、 この順番で撮った、ベクトルと呼ばれます、 長さそれは数値的には 平行四辺形の面積に等しい、これらのベクトルに基づいて構築されます。 ベクター ベクトルに直交、基底が正しい方向になるように指示されます。 
骨ごとに定義を分析してみると、面白いことがたくさんあります！
したがって、次の重要な点を強調できます。
1) 定義により、赤い矢印で示されるソース ベクトル 同一線上にない。 共線ベクトルの場合については、少し後で検討するのが適切でしょう。
2) 取得されたベクトル 厳格な順序で: – 「a」に「be」を掛けます、「be」から「a」ではありません。 ベクトル乗算の結果は VECTOR で、青で示されています。 ベクトルを逆の順序で乗算すると、長さが同じで方向が逆のベクトル (深紅色) が得られます。 つまり平等です 
.
3) 次に、ベクトル積の幾何学的意味を理解しましょう。 これはとても重要なポイントです！ 青色のベクトル (したがって、深紅色のベクトル ) の長さは、ベクトル上に構築された平行四辺形の面積と数値的に等しくなります。 図では、この平行四辺形を黒の網掛けで示しています。
ノート ：図面は概略図であり、当然のことながら、外積の公称長さは平行四辺形の面積と等しくありません。
幾何学的公式の 1 つを思い出してください。 平行四辺形の面積は、隣接する辺とそれらの間の角度の正弦の積に等しい。 したがって、上記に基づいて、ベクトル積の LENGTH を計算する式は有効です。
この式では、ベクトル自体についてではなく、ベクトルの長さについて話していることを強調します。 実用的な意味は何でしょうか？ そして、その意味は、解析幾何学の問題では、ベクトル積の概念を通じて平行四辺形の面積がしばしば見つかるようなものです。
2 番目の重要な式が得られます。 平行四辺形の対角線 (赤い点線) は、それを 2 つの等しい三角形に分割します。 したがって、ベクトル（赤い陰影）に基づいて構築された三角形の面積は、次の式で求めることができます。
4) 同様に重要な事実は、ベクトルがベクトルに直交しているということです。 
。 もちろん、逆向きのベクトル (深紅の矢印) も元のベクトルと直交します。
5) ベクトルは次のように方向付けられます。 基礎それは持っています 右オリエンテーション。 についてのレッスンで 新しい基盤への移行について詳しくお話しました 面方位、そして今度は空間の向きが何であるかを理解します。 あなたの指で説明します 右手。 精神的に組み合わせる 人差し指ベクトルと 中指ベクトル付き。 薬指と小指手のひらに押し込みます。 結果として 親指- ベクトル積が検索されます。 これが右向きの基本です（図にあります）。 ここでベクトルを交換します ( 人差し指と中指) 場所によっては、その結果、親指が向きを変え、ベクトル積がすでに下を向くようになります。 これも右指向の根拠です。 おそらく、あなたは疑問を持っているかもしれません：左向きはどのような根拠に基づいて決められていますか？ 同じ指を「割り当てる」 左手ベクトルを取得し、左基底と左空間方向を取得します。 (この場合、親指は下のベクトルの方向に配置されます)。 比喩的に言えば、これらのベースは空間を「ねじる」、つまり空間を異なる方向に向けます。 そして、この概念は、突飛な、または抽象的なものと考えるべきではありません。たとえば、最も普通の鏡は空間の方向を変えますが、「反射した物体を鏡から引き出す」場合、一般的には次のことはできません。それを「オリジナル」と組み合わせます。 ちなみに、鏡に3本の指を持ってきて、反射を分析してください ;-)
...今知ったことは、なんと素晴らしいことでしょう。 右向きと左向き根拠は、方向性の変更に関する一部の講師の発言がひどいためです =)
定義は詳細に検討されていますが、ベクトルが同一線上にある場合に何が起こるかを解明することはまだ残っています。 ベクトルが同一線上にある場合、ベクトルを 1 つの直線上に配置することができ、平行四辺形も 1 つの直線に「折り畳まれます」。 数学者が言うように、そのような領域は、 退化する平行四辺形はゼロです。 式からも同じことがわかります - 0 または 180 度の正弦は 0 に等しく、これは面積が 0 であることを意味します。
したがって、 の場合、 
と 
。 外積自体はゼロベクトルに等しいことに注意してください。しかし、実際にはこれは無視されることが多く、これもゼロに等しいと書かれています。
特殊なケースは、ベクトルとそれ自体のベクトル積です。
外積を使用すると、3 次元ベクトルの共線性を確認できます。この問題なども解析します。
実際の例を解決するには、次のことが必要になる場合があります。 三角関数表そこからサインの値を見つけます。
さて、火を起こしましょう。
例1
a) 次の場合、ベクトルのベクトル積の長さを求めます。 
b) 次の場合、ベクトルに基づいて構築された平行四辺形の面積を求めます。 
解決：いいえ、これはタイプミスではなく、条件項目の初期データを意図的に同じにしました。 なぜなら、ソリューションの設計が異なるからです。
a) 条件に応じて、次のことを見つける必要があります。 長さベクトル (ベクトル積)。 対応する式によると、次のようになります。
答え:
長さについて尋ねられたので、答えでは寸法 - 単位を示します。
b) 条件に応じて、次のことを見つける必要があります。 四角ベクトルに基づいて構築された平行四辺形。 この平行四辺形の面積は、数値的には外積の長さに等しいです。
答え:
ベクター製品についての回答にはまったく触れられていないことに注意してください。 図形エリア、それぞれ、寸法は正方形単位です。
条件から何が求められているかを常に考え、それに基づいて定式化します。 クリア答え。 文字通りの文言のように思えるかもしれないが、教師の中には文語主義者が十分にいるので、可能性の高い課題は修正のために返却されるだろう。 これは特に厳しい指摘ではありませんが、答えが間違っていると、その人は単純なことを理解していないか、タスクの本質を理解していないか、あるいはその両方であるという印象を受けます。 高等数学や他の科目の問題を解く際には、この瞬間を常にコントロールする必要があります。
大きな文字「en」はどこへ行ったのでしょうか？ 原則として、ソリューションにさらに固執することもできますが、記録を短縮するために、そうしませんでした。 それは皆さんも御理解いただきたいと思いますし、同じものを指定しているということでございます。
DIY ソリューションの一般的な例:
例 2
次の場合、ベクトルに基づいて構築された三角形の面積を求めます。 
ベクトル積によって三角形の面積を求める公式は、定義のコメントに示されています。 レッスンの最後に解答と答えを示します。
実際には、このタスクは非常に一般的であり、三角形は一般に拷問される可能性があります。
他の問題を解決するには、次のものが必要です。
ベクター製品のいくつかの特性についてはすでに検討しましたが、このリストに含めておきます。
任意のベクトルと任意の数値については、次のプロパティが当てはまります。
1) 他の情報源では、この項目は通常、その特性が区別されていませんが、実際には非常に重要です。 それで、それをそのままにしておきます。
2) 
- このプロパティについては上でも説明していますが、次のように呼ばれることもあります。 反可換性。 言い換えれば、ベクトルの順序が重要です。
3) - 組み合わせまたは 連想的なベクトル積法。 定数はベクトル積の制限外に簡単に取り出されます。 本当に、彼らはそこで何をしているのでしょうか？
4) - 配布または 分布ベクトル積法。 ブラケットの開きも問題ありません。
デモンストレーションとして、短い例を考えてみましょう。
例 3
どうかを見つける 
解決：条件によっては、ベクトル積の長さを求めることが再度必要になります。 ミニチュアをペイントしましょう: 
(1) 結合法則に従って、ベクトル積の限界を超える定数を取り出します。
(2) モジュールから定数を取り出しますが、モジュールはマイナス記号を「食べます」。 長さを負にすることはできません。
(3) 以下のことは明らかです。
答え: 
火に薪を投げる時が来ました。
例 4
次の場合、ベクトルに基づいて構築された三角形の面積を計算します。 
解決：公式を使用して三角形の面積を求めます 
。 問題は、ベクトル「ce」と「te」自体がベクトルの合計として表されることです。 ここでのアルゴリズムは標準的なもので、レッスンの例 3 と 4 をいくらか思い出させます。 ベクトルの内積。 わかりやすくするために、3 つのステップに分けてみましょう。
1) 最初のステップでは、ベクター積を介してベクター積を表現します。実際には、 ベクトルをベクトルで表現する。 長さについてはまだ発表されていません！
(1) ベクトルの式を代入します。
(2) 分配法則を使用して、多項式の乗算の規則に従って括弧を開きます。
(3) 結合法則を使用して、ベクトル積を超える定数をすべて取り出します。 経験が少なくても、アクション 2 と 3 を同時に実行できます。
(4) 最初と最後の項は、快適な性質によりゼロ (ゼロ ベクトル) に等しくなります。 2 番目の項では、ベクトル積の反可換性特性を使用します。
(5) 類似の用語を紹介します。
その結果、ベクターはベクターを介して発現されることが判明しました。これは、達成するために必要なことでした。 
2) 2 番目のステップでは、必要なベクトル積の長さを見つけます。 このアクションは例 3 に似ています。 
3) 必要な三角形の面積を求めます。 
ソリューションのステップ 2 ～ 3 は 1 行に配置できます。
答え:
検討されている問題はテストでは非常に一般的なもので、独立した解決策の例を次に示します。
例5
どうかを見つける
短い解答とレッスンの最後に解答。 前の例を研究するときにどれだけ注意力を払ったか見てみましょう ;-)
式は非常に単純です。行列式の一番上の行に座標ベクトルを書き、2 行目と 3 行目にベクトルの座標を「パック」し、 厳密な順序で- 最初にベクトル「ve」の座標、次にベクトル「double-ve」の座標。 ベクトルを別の順序で乗算する必要がある場合は、行も交換する必要があります。 
例 10
次の空間ベクトルが同一線上にあるかどうかを確認します。
A)
b) 
解決: このテストは、このレッスンのステートメントの 1 つに基づいています: ベクトルが共線性がある場合、その外積はゼロ (ゼロ ベクトル) です。 
.
a) ベクトル積を見つけます。 
したがって、ベクトルは同一線上にありません。
b) ベクトル積を見つけます。 
答え: a) 同一線上にない、b)
おそらくここに、ベクトルのベクトル積に関するすべての基本情報が記載されています。
ベクトルの混合積が使用される問題はほとんどないため、このセクションはそれほど大きくなりません。 実際、すべては定義、幾何学的意味、およびいくつかの実用的な公式に基づいています。
ベクトルの混合積は 3 つのベクトルの積です:
こうして彼らは電車のように並んで待ちます、計算されるまで待ちきれません。
まず最初にもう一度定義とイメージを示します。
意味：混合品 非共面上ベクトル、 この順番で撮った、と呼ばれます 直方体の体積、これらのベクトルに基づいて構築され、基底が右の場合は「+」記号が、基底が左の場合は「-」記号が付けられます。
絵を描いてみましょう。 私たちには見えない線は点線で描かれています。 
定義を詳しく見てみましょう。
2) 取得されたベクトル 特定の順序でつまり、ご想像のとおり、積内のベクトルの順列には結果が伴います。
3) 幾何学的意味についてコメントする前に、明白な事実に注意してください。 ベクトルの混合積は NUMBER です: 。 教育関連の文献では、デザインは多少異なる場合があります。以前は、混合製品を介して、計算結果を「pe」という文字で指定していました。
A優先 混合積は直方体の体積です、ベクトルに基づいて構築されています (図は赤いベクトルと黒い線で描かれています)。 つまり、その数は指定された平行六面体の体積に等しくなります。
ノート ：図は概略図です。
4) 基底と空間の方向の概念を再び気にするのはやめましょう。 最後の部分の意味は、ボリュームにマイナス記号を追加できることです。 簡単に言えば、混合積は負になる可能性があります。
ベクトルに基づいて構築された平行六面体の体積を計算する式は、定義から直接導き出されます。
明らかに、外積の場合、ベクトルが取得される順序が重要になります。
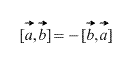
また、定義から直接、任意のスカラー因数 k (数値) について次のことが当てはまります。
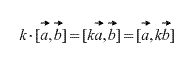
共線ベクトルの外積はゼロ ベクトルに等しくなります。 さらに、2 つのベクトルの外積は、それらが同一線上にある場合にのみゼロになります。 (それらの 1 つがゼロ ベクトルの場合、定義上、ゼロ ベクトルは任意のベクトルと同一直線上にあることを覚えておく必要があります)。
ベクター製品には、 分配財産、 あれは
ベクトルの座標による外積の表現。
2 つのベクトルが与えられるとします
(始点と終点の座標によってベクトルの座標を見つける方法 - 記事「ベクトルのドット積」の段落「ドット積の代替定義」または座標によって与えられる 2 つのベクトルのドット積の計算を参照してください。)
なぜベクター製品が必要なのでしょうか?
外積を使用するにはさまざまな方法があります。たとえば、すでに上で説明したように、2 つのベクトルの外積を計算することによって、それらが共線的であるかどうかを確認できます。
または、これらのベクトルから構築される平行四辺形の面積を計算する方法として使用できます。 定義に基づいて、結果のベクトルの長さはこの平行四辺形の面積になります。
また、電気や磁気にも膨大な数の応用分野が存在します。ベクトル積のオンライン計算機。
この計算機を使用して 2 つのベクトルのスカラー積を求めるには、最初のベクトルの座標を最初の行に順番に入力し、2 番目のベクトルの座標を 2 番目の行に入力する必要があります。 ベクトルの座標は、開始座標と終了座標から計算できます (記事を参照) ベクトルのドット積 、 item ドット積の代替定義、または座標が指定された 2 つのベクトルのドット積の計算。)
