Pont termék tulajdonságai
Vektorok, definíciók, tulajdonságok pontszorzata
Lineáris műveletek vektorokon.
Vektorok, alapfogalmak, definíciók, lineáris műveletek rajtuk
Egy vektor egy síkon a pontjainak rendezett párja, míg az első pontot a vektor kezdetének, a másodikat a végének nevezzük.
Két vektort egyenlőnek nevezünk, ha egyenlők és egyirányúak.
Azokat a vektorokat, amelyek ugyanazon a vonalon helyezkednek el, koirányú irányúnak nevezzük, ha egyirányúak ugyanazon vektorral, amely nem ezen az egyenesen fekszik.
Azokat a vektorokat, amelyek ugyanazon az egyenesen vagy párhuzamos egyeneseken helyezkednek el, kollineárisnak, a kollineáris, de nem társirányú vektorokat ellentétes irányúnak nevezzük.
A merőleges vonalakon fekvő vektorokat ortogonálisnak nevezzük.
Meghatározás 5.4. összeg a+b vektorok a És b a vektor elejétől jövő vektornak nevezzük A a vektor végére b , ha a vektor eleje b egybeesik a vektor végével A .
Meghatározás 5.5. különbség a - b vektorok A És b egy ilyen vektort nevezünk Val vel , amely a vektorral együtt b vektort ad A .
Meghatározás 5.6. munkak a vektor A számonként k vektornak nevezzük b , kollineáris vektor A , amelynek modulja egyenlő | k||a |, és egy irány, amely megegyezik az iránnyal A nál nél k>0 és az ellenkezője A nál nél k<0.
Egy vektor számmal való szorzásának tulajdonságai:
1. tulajdonság. k(a+b ) = k a+ k b.
2. tulajdonság. (k+m)a = k a+ m a.
3. tulajdonság. k(m a) = (km)a .
Következmény. Ha nem nulla vektorok A És b kollineárisak, akkor van egy szám k, Mit b= k a.
Két nullától eltérő vektor skaláris szorzata aÉs b számnak (skalárnak) nevezzük, amely egyenlő ezen vektorok hosszának és a közöttük lévő φ szög koszinuszának szorzatával. A skaláris szorzat többféleképpen is kifejezhető, például mint ab, a · b, (a , b), (a · b). Tehát a ponttermék:
a · b = |a| · | b| cos φ
Ha legalább az egyik vektor egyenlő nullával, akkor a skaláris szorzat egyenlő nullával.
Permutációs tulajdonság: a · b = b · a(a skaláris szorzat nem változik a tényezők permutációjától);
elosztási tulajdonság: a · ( b · c) = (a · b) · c(az eredmény nem függ a szorzás sorrendjétől);
Kombinációs tulajdonság (a skaláris tényezőhöz viszonyítva): (λ a) · b = λ ( a · b).
Az ortogonalitás (merõlegesség) tulajdonsága: ha a vektor aÉs b nem nulla, akkor pontszorzatuk csak akkor nulla, ha ezek a vektorok merőlegesek (egymásra merőlegesek) a ┴ b;
Négyzet alakú ingatlan: a · a = a 2 = |a| 2 (egy vektor skaláris szorzata önmagával egyenlő a modulusának négyzetével);
Ha a vektorok koordinátái a=(x 1 , y 1 , z 1 ) és b=(x 2 , y 2 , z 2 ), akkor a skaláris szorzat az a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .
Vektor gazdaság vektorok. Meghatározás: Két vektor vektorszorzata, és olyan vektorként értendő, amelyre:
A modul egyenlő az ezekre a vektorokra épített paralelogramma területével, azaz. , ahol az és a vektorok közötti szög
Ez a vektor merőleges a szorzott vektorokra, azaz.
Ha a vektorok nem kollineárisak, akkor a vektorok jobboldali hármasát alkotják.
Kereszttermék tulajdonságai:
1. A faktorok sorrendjének megváltoztatásakor a vektorszorzat az ellenkezőjére változtatja az előjelét, megőrzi a modult, azaz.
2 .A vektornégyzet egyenlő a nulla-vektorral, azaz.
3 .A skaláris tényező a vektorszorzat előjeléből kivehető, azaz.
4 .Bármely három vektorra az egyenlőség
5 .Szükséges és elégséges feltétele két vektor kollinearitása és :
Meghatározás. Az a és b vektor vektorszorzata a [«, b] (vagy l x b) szimbólummal jelölt vektor úgy, hogy 1) az [a, b] vektor hossza egyenlő (p, ahol y az a és b (31) vektorok közötti szög 2) az [a, b) vektor merőleges az a és b vektorokra, azaz. merőleges ezen vektorok síkjára; 3) az [a, b] vektor úgy van irányítva, hogy ennek a vektornak a végétől a legrövidebb fordulat a-ból b-be az óramutató járásával ellentétes irányban történik (32. ábra). Rizs. 32 31. ábra Más szóval az a, b és [а, b) vektorok alkotják a vektorok jobb oldali hármasát, azaz. a jobb kéz hüvelyk-, mutató- és középső ujjához hasonlóan helyezkedik el. Ha az a és b vektorok kollineárisak, akkor azt feltételezzük, hogy [a, b] = 0. Definíció szerint a vektorszorzat hossza numerikusan egyenlő a szorzott vektorokra épített paralelogramma Sa területével (33. ábra). a és b, mint az oldalakon: 6.1 . Egy vektorszorzat tulajdonságai 1. Egy vektorszorzat akkor és csak akkor egyenlő nulla vektorral, ha a szorzott vektorok legalább egyike nulla, vagy ha ezek a vektorok kollineárisak (ha az a és b vektorok kollineárisak, akkor a köztük lévő szög vagy 0 vagy 7r). Ez könnyen megállapítható abból, hogy Ha a nulla vektort kollinzárnak tekintjük bármely vektorhoz, akkor az a és b vektorok kollináris feltétele a következőképpen fejezhető ki 2. A vektorszorzat antikommutatív, azaz mindig. Valójában az (a, b) és a vektorok azonos hosszúságúak és kollineárisak. Ezeknek a vektoroknak az iránya ellentétes, mivel az [a, b] vektor végétől a legrövidebb fordulat a-ból b-be az óramutató járásával ellentétes irányban, a [b, a] vektor végétől pedig az óramutató járásával megegyezően látható (ábra). 34). 3. A vektorszorzat eloszlási tulajdonsággal rendelkezik az összeadáshoz képest 4. Az A numerikus tényező kivehető a vektorszorzat előjeléből 6.2. A koordinátákkal megadott vektorok vektorszorzata Adjuk meg az a és b vektorokat a bázis koordinátáival. A vektorszorzat eloszlási tulajdonságát felhasználva megtaláljuk a koordinátákkal megadott vektorok vektorszorzatát. Vegyes munka. Írjuk ki a koordináta ortok vektorszorzatait (35. ábra): Ezért az a és b vektor vektorszorzatára a (3) képletből a következő kifejezési determinánst kapjuk az 1. sor elemei felett, kapjuk ( 4). Példák. 1. Keresse meg a vektorokra épített paralelogramma területét! Keresse meg a háromszög területét (36. ábra). Nyilvánvaló, hogy a JSC háromszög b "d területe egyenlő az O AC B paralelogramma S területének felével. A vektorszorzat kiszámítása (a, b | az a \u003d OA és b \u003d b \u003d ob vektorok ), megkapjuk (a, b), c) = [a, |b, c)) általános esetben nem igaz. Például a = ss j-re van § 7. Vektorok vegyes szorzata Legyen három vektor a, b és c. Az a és 1> vektorokat vektorosan megszorozzuk. Eredményként megkapjuk az [a, 1>] vektort. Megszorozzuk skalárisan a c vektorral: (k b), c A szám ( [a, b], e) az a, b. c vektorok vegyes szorzatának nevezzük, és az (a, 1), e szimbólummal jelöljük 7.1. A vegyes szorzat geometriai jelentése Tegyük félre a vektorok a, b és az általános O pontból (37. ábra) Ha mind a négy O, A, B, C pont ugyanabban a síkban van (az a, b és c vektorokat ebben az esetben koplanárisnak nevezzük), akkor a vegyes szorzat ([a, b], c) = 0. Ez abból a tényből következik, hogy az [a, b| vektor merőleges arra a síkra, amelyben az a és 1 vektorok fekszenek ”, és innen a c vektor. / Ha a Az O, A, B, C pontok nem egy síkban fekszenek (az a, b és c vektorok nem egysíkúak), az OA, OB és OS élekre paralelepipedont építünk (ábra). 38 a). A keresztszorzat definíciója szerint van (a,b) = So c, ahol So az OADB paralelogramma területe, és c egy egységvektor, amely merőleges az a és b vektorokra, és olyan, hogy az a hármas , b, c helyes, azaz. az a, b és c vektorok a jobb kéz hüvelyk-, mutató- és középső ujjaként helyezkednek el (38. b ábra). A jobb oldali skaláron lévő utolsó egyenlőség mindkét részét megszorozva c vektorral, azt kapjuk, hogy a koordinátákkal megadott vektorok vektorszorzata. Vegyes munka. Az rc c szám egyenlő a megszerkesztett paralelepipedon h magasságával, a „+” jellel felvéve, ha a c és c vektorok közötti szög hegyesszögű (az a, b, c hármas helyes), és a „ -” ha a szög tompaszögű (az a, b, c hármas - balra), így tehát az a, b és c vektorok vegyes szorzata egyenlő az ezekre a vektorokra, mint az élekre épített paralelepipedon V térfogatával. ha az a, b, c hármas jobb, és -V, ha az a , b, c hármas - bal. A vegyes szorzat geometriai jelentése alapján arra a következtetésre juthatunk, hogy ugyanazokat a, b és c vektorokat bármilyen más sorrendben megszorozva mindig vagy +7-et vagy -K-t kapunk. A pro- Fig. 38 referencia csak attól függ, hogy a szorzott vektorok melyik triplettet alkotják – jobbra vagy balra. Ha az a, b, c vektorok jobboldali hármast alkotnak, akkor a b, c, a és c, a, b hármasok is helyesek lesznek. Ugyanakkor mindhárom hármas b, a, c; a, c, b és c, b, a - balra. Így (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , A). Még egyszer hangsúlyozzuk, hogy a vektorok vegyes szorzata akkor és csak akkor egyenlő nullával, ha az a, b, c szorzott vektorok egysíkúak: (a, b, c egysíkúak) 7.2. Koordináták vegyes szorzata Adjuk meg az a, b, c vektorokat koordinátáikkal az i, j, k bázisban: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Keressünk kifejezést vegyes szorzatukra (a, b, c). Az i, J, k bázisban a koordinátáik alapján megadott vektorok vegyes szorzata van, amely egyenlő a harmadrendű determinánssal, amelynek sorai rendre a szorzott első, második és harmadik koordinátáiból állnak. vektorok. Az a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) vektorok kompaniritásának szükséges és elégséges feltétele a következő formában írható fel z, ar2 y2-2 =0. Uz Példa. Ellenőrizze, hogy a v = (7,4,6), b = (2, 1,1), c = (19, II, 17) vektorok síkbeliek-e. A vizsgált vektorok egysíkúak vagy nem egysíkúak lesznek, attól függően, hogy a determináns egyenlő-e nullával vagy sem.Az első sor elemeire kibontva azt kapjuk, hogy 7.3. Kettős keresztszorzat A kettős keresztszorzat [a, [b, c]] egy vektor, amely merőleges az a és [b, c] vektorokra. Ezért a b és c vektorok síkjában fekszik, és ezekben a vektorokban bővíthető. Megmutatható, hogy az [a, [!>, c]] = b(a, e) - c(a, b) képlet érvényes. Gyakorlatok 1. Három vektor AB = c, W? = o és CA = b a háromszög oldalai. Fejezzük ki a, b és c értékekkel a háromszög AM, DN, CP mediánjával egybeeső vektorokat. 2. Milyen feltételt kell összekapcsolni a p és q vektorok között, hogy a p + q vektor kettéosztja a köztük lévő szöget? Feltételezzük, hogy mindhárom vektor egy közös origóhoz kapcsolódik. 3. Számítsa ki az a = 5p + 2q és b = p - 3q vektorokra épített paralelogramma átlóinak hosszát, ha ismert, hogy |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. A rombusz közös csúcsból kilépő oldalait a és b-vel jelölve igazoljuk, hogy a rombusz átlói egymásra merőlegesek. 5. Számítsa ki az a = 4i + 7j + 3k és a b = 31 - 5j + k vektorok pontszorzatát! 6. Keresse meg az a = (6, 7, -6) vektorral párhuzamos a0 egységvektort! 7. Határozza meg az a = l+ j- kHa vektor vetületét b = 21 - j - 3k vektor! 8. Határozza meg az IS "w vektorok közötti szög koszinuszát, ha A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Keressünk egy p° egységvektort, amely egyidejűleg merőleges az a = (3, 6, 8) vektorra és az x tengelyre! 10. Számítsa ki az a = 2i+J-k, b=i-3j + k vektorokra épített paralelofam átlói közötti szög szinuszát, mint az oldalakon! Számítsd ki az a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k vektorokra épített paraleleogramma h magasságát, ha az a és I vektorokra épített paralelogrammát vesszük alapul! Válaszok
Szög vektorok között
Ahhoz, hogy bemutassuk a két vektor keresztszorzatának fogalmát, először foglalkoznunk kell egy olyan fogalommal, mint a vektorok közötti szög.
Adjunk két vektort $\overline(α)$ és $\overline(β)$. Vegyünk egy $O$ pontot a térben, és tegyük félre a $\overline(α)=\overline(OA)$ és a $\overline(β)=\overline(OB)$ vektorokat, majd a $AOB szöget. $-t ezen vektorok közötti szögnek nevezzük (1. ábra).
Jelölés: $∠(\overline(α),\overline(β))$
1. definíció
Két vektor vektorszorzata egy olyan vektor, amely merőleges mindkét adott vektorra, és a hossza egyenlő lesz ezen vektorok hosszának szorzatával a vektorok közötti szög szinuszával, és ez a vektor két kezdeti vektorral azonos orientáció, mint a derékszögű koordináta-rendszer.
Jelölés: $\overline(α)х\overline(β)$.
Matematikailag így néz ki:
Nyilvánvaló, hogy a vektorok külső szorzata két esetben egyenlő lesz a nulla vektorral:
Ha világosan látni szeretné, hogyan található a vektorok keresztszorzata, tekintse meg a következő megoldási példákat.
1. példa
Határozza meg a $\overline(δ)$ vektor hosszát, amely a vektorok keresztszorzatának eredménye lesz, a $\overline(α)=(0,4,0)$ és $\overline(β) koordinátákkal. =(3,0,0 )$.
Megoldás.
Ábrázoljuk ezeket a vektorokat a derékszögű koordinátatérben (3. ábra):
3. ábra Vektorok derékszögű koordinátatérben. Author24 - hallgatói dolgozatok online cseréje
Látjuk, hogy ezek a vektorok az $Ox$ és a $Oy$ tengelyeken fekszenek. Ezért a köztük lévő szög 90$^\circ$ lesz. Nézzük meg ezeknek a vektoroknak a hosszát:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Ezután az 1. definíció alapján megkapjuk a $|\overline(δ)|$ modult
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Válasz: 12 dollár.
Az 1. definíció azonnal magában foglalja a két vektor keresztszorzatának megtalálásának módját. Mivel egy vektornak az érték mellett iránya is van, lehetetlen csak skaláris értékkel megtalálni. De emellett van egy másik módja is annak, hogy a koordináták segítségével megtaláljuk a nekünk adott vektorokat.
Adjuk meg a $\overline(α)$ és $\overline(β)$ vektorokat, amelyeknek $(α_1,α_2,α_3)$ és $(β_1,β_2,β_3)$ koordinátái lesznek. Ekkor a keresztszorzat vektora (nevezetesen a koordinátái) megtalálható a következő képlettel:
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
Ellenkező esetben a determinánst kibővítve a következő koordinátákat kapjuk
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
2. példa
Keresse meg a $\overline(α)$ és $\overline(β)$ kollineáris vektorok keresztszorzatának vektorát $(0,3,3)$ és $(-1,2,6)$ koordinátákkal.
Megoldás.
Használjuk a fenti képletet. Kap
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
Válasz: $(12,-3,3)$.
A $\overline(α)$, $\overline(β)$ és $\overline(γ)$, valamint a $r∈R$ tetszőleges kevert három vektorra a következő tulajdonságok érvényesek:
3. példa
Keresse meg a paralelogramma területét, amelynek csúcsai $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ és $(3,8,0) koordinátákkal rendelkeznek. $.
Megoldás.
Először rajzolja meg ezt a paralelogrammát a koordinátatérben (5. ábra):
5. ábra Párhuzamos a koordinátatérben. Author24 - hallgatói dolgozatok online cseréje
Látjuk, hogy ennek a paralelogrammának a két oldala a $\overline(α)=(3,0,0)$ és a $\overline(β)=(0,8,0)$ koordinátákkal rendelkező kollineáris vektorok felhasználásával készült. A negyedik tulajdonságot használva a következőket kapjuk:
$S=|\overline(α)x\overline(β)|$
Keresse meg a $\overline(α)х\overline(β)$ vektort:
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Ennélfogva
$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$
Ebben a leckében további két műveletet nézünk meg vektorokkal: vektorok keresztszorzataÉs vektorok vegyes szorzata (azonnali link akinek szüksége van rá). Nem baj, néha megesik, hogy a teljes boldogság érdekében, ráadásul vektorok pontszorzata, egyre többre van szükség. Ilyen a vektorfüggőség. Az embernek az a benyomása lehet, hogy az analitikus geometria dzsungelébe kerülünk. Ez rossz. A felsőbb matematikának ebben a részében általában kevés a tűzifa, kivéve talán elég Pinokkiót. Valójában az anyag nagyon gyakori és egyszerű – aligha bonyolultabb, mint ugyanaz skaláris szorzat, még kevesebb tipikus feladat is lesz. A legfontosabb dolog az analitikus geometriában, amint azt sokan látják vagy már látták, az, hogy NE VEGYE KI A SZÁMÍTÁSOKAT. Ismételd, mint egy varázslatot, és boldog leszel =)
Ha valahol távol csillognak a vektorok, mint a villám a láthatáron, nem számít, kezdje a leckével Vektorok bábokhoz a vektorokkal kapcsolatos alapvető ismeretek helyreállítása vagy visszaszerzése. A felkészültebb olvasók szelektíven ismerkedhetnek meg az információkkal, igyekeztem a gyakorlati munkában gyakran fellelhető legteljesebb példagyűjteményt összegyűjteni.
Mitől leszel boldog? Kicsi koromban két, sőt három labdával is tudtam zsonglőrködni. Jól sikerült. Most már egyáltalán nem kell zsonglőrködni, hiszen megfontoljuk csak térvektorok, és a két koordinátájú lapos vektorok kimaradnak. Miért? Így születtek ezek az akciók - a vektorok és a vektorok vegyes szorzata definiálva és háromdimenziós térben működik. Már könnyebb!
Ebben a műveletben, ugyanúgy, mint a skaláris szorzatnál, két vektor. Legyenek múlhatatlan betűk.
Maga az akció jelöljük a következő módon: . Vannak más lehetőségek is, de én a vektorok keresztszorzatát szoktam így jelölni, szögletes zárójelben kereszttel.
És azonnal kérdés: ha bent vektorok pontszorzata két vektorról van szó, és itt is két vektort szorozunk, akkor mi a különbség? Egyértelmű különbség mindenekelőtt az EREDMÉNYBEN:
A vektorok skaláris szorzatának eredménye egy SZÁM:
A vektorok keresztszorzatának eredménye egy VEKTOR: , azaz megszorozzuk a vektorokat és ismét vektort kapunk. Zárt klub. Valójában innen ered a művelet neve. A különböző oktatási irodalomban a megnevezések is változhatnak, én a betűt használom.
Először lesz egy definíció képpel, majd kommentek.
Meghatározás: kereszttermék nem kollineáris vektorok, ebben a sorrendben szedve, a neve VECTOR, hossz ami számszerűen egyenlő a paralelogramma területével, ezekre a vektorokra épül; vektor merőleges a vektorokra, és úgy van irányítva, hogy az alap megfelelő tájolású legyen:
A meghatározást csontok szerint elemezzük, sok érdekesség van!
Tehát a következő lényeges pontokat emelhetjük ki:
1) Forrásvektorok, definíció szerint piros nyilakkal jelölve nem kollineáris. A kollineáris vektorok esetét egy kicsit később célszerű megvizsgálni.
2) Felvett vektorok szigorú sorrendben: – "a" szorozva "be", nem a "legyen" "a"-ra. A vektorszorzás eredménye a VECTOR , amelyet kékkel jelölünk. Ha a vektorokat fordított sorrendben szorozzuk, akkor egyenlő hosszúságú és ellentétes irányú (bíbor színű) vektort kapunk. Vagyis az egyenlőség 
.
3) Most ismerkedjünk meg a vektorszorzat geometriai jelentésével. Ez egy nagyon fontos szempont! A kék vektor HOSSZA (és így a bíbor vektor) numerikusan egyenlő a vektorokra épített paralelogramma TERÜLETÉVEL. Az ábrán ez a paralelogramma feketével van árnyékolva.
jegyzet : a rajz sematikus, és természetesen a keresztszorzat névleges hossza nem egyenlő a paralelogramma területével.
Emlékezzünk az egyik geometriai képletre: a paralelogramma területe egyenlő a szomszédos oldalak és a köztük lévő szög szinuszának szorzatával. Ezért a fentiek alapján a vektorszorzat HOSSZ-számítási képlete érvényes:
Hangsúlyozom, hogy a képletben a vektor HOSSZÁRÓL van szó, és nem magáról a vektorról. Mi a gyakorlati jelentése? A jelentése pedig olyan, hogy az analitikus geometria problémáiban a paralelogramma területét gyakran a vektorszorzat fogalmán keresztül találják meg:
Megkapjuk a második fontos képletet. A paralelogramma átlója (piros pontozott vonal) két egyenlő háromszögre osztja. Ezért a vektorokra épített háromszög területe (piros árnyékolás) a következő képlettel kereshető:
4) Ugyanilyen fontos tény, hogy a vektor ortogonális a vektorokra, azaz 
. Természetesen az ellentétes irányú vektor (bíbor nyíl) is merőleges az eredeti vektorokra.
5) A vektort úgy irányítjuk, hogy alapján Megvan jobb irányultság. Egy leckében kb áttérni egy új alapra részletesen beszéltem róla sík tájolás, és most kitaláljuk, mi a tér tájolása. Az ujjadon elmagyarázom jobb kéz. Szellemileg kombinálni mutatóujj vektorral és középső ujj vektorral. Gyűrűsujj és kisujj nyomd a tenyeredbe. Ennek eredményeként hüvelykujj- a vektorszorzat felfelé néz. Ez a jobboldali alap (az ábrán látható). Most cserélje fel a vektorokat ( mutató és középső ujj) helyenként ennek hatására a hüvelykujj megfordul, és a vektorszorzat máris lefelé néz. Ez is egy jobboldali alap. Talán van egy kérdés: mi alapján áll a baloldali irányultság? "Hozzárendelni" ugyanazokat az ujjakat bal kéz vektorokat, és megkapja a bal bázist és a bal térbeli tájolást (ebben az esetben a hüvelykujj az alsó vektor irányába fog elhelyezkedni). Képletesen szólva ezek az alapok különböző irányokba „csavarják” vagy orientálják a teret. És ezt a koncepciót nem szabad távolinak vagy elvontnak tekinteni - például a leghétköznapibb tükör megváltoztatja a tér tájolását, és ha „kihúzza a visszavert tárgyat a tükörből”, akkor általában nem lesz lehetséges kombinálja az „eredetivel”. Mellesleg, vidd három ujjad a tükörhöz, és elemezd a visszaverődést ;-)
... milyen jó, hogy most már tudsz róla jobbra és balra orientált alapokon, mert borzasztóak egyes előadók kijelentései az irányváltásról =)
A definíciót részletesen kidolgoztuk, még ki kell deríteni, mi történik, ha a vektorok kollineárisak. Ha a vektorok kollineárisak, akkor egy egyenesre helyezhetők, és a paralelogrammánk is egy egyenesbe „gyűrődik”. Az ilyenek területe, ahogy a matematikusok mondják, elfajzott paralelogramma nulla. Ugyanez következik a képletből - a nulla vagy 180 fok szinusza egyenlő nullával, ami azt jelenti, hogy a terület nulla
Így ha , akkor 
És 
. Vegye figyelembe, hogy maga a keresztszorzat egyenlő a nulla vektorral, de a gyakorlatban ezt gyakran figyelmen kívül hagyják, és azt írják, hogy ez is egyenlő nullával.
Egy speciális eset egy vektor és önmagának vektorszorzata:
A keresztszorzat segítségével ellenőrizhető a háromdimenziós vektorok kollinearitása, és többek között ezt a problémát is elemezzük.
A gyakorlati példák megoldásához szükséges lehet trigonometrikus táblázat hogy kikeresse belőle a szinuszok értékeit.
Nos, gyújtsunk tüzet:
1. példa
a) Határozza meg a vektorok vektorszorzatának hosszát, ha 
b) Határozza meg a vektorokra épített paralelogramma területét, ha 
Megoldás: Nem, ez nem elírás, szándékosan tettem azonossá a kezdeti adatokat a feltételelemekben. Mert a megoldások kialakítása más lesz!
a) A feltétel szerint meg kell találni hossz vektor (vektorszorzat). A megfelelő képlet szerint:
Válasz:
Mivel a hosszra kérdezték, a válaszban megadjuk a méretet - mértékegységeket.
b) A feltétel szerint meg kell találni négyzet vektorokra épített paralelogramma . Ennek a paralelogrammának a területe számszerűen megegyezik a keresztszorzat hosszával:
Válasz:
Felhívjuk figyelmét, hogy a vektoros szorzatra adott válaszban egyáltalán nem esik szó, arról kérdeztünk ábra terület, illetve a méret négyzetegység.
Mindig megnézzük, hogy a feltétel MIT igényel, és ennek alapján fogalmazunk egyértelmű válasz. Lehet, hogy szószerintiségnek tűnik, de a tanárok között van elég literalista, és a feladat jó eséllyel visszakerül átdolgozásra. Bár ez nem egy különösebben megerőltető trükk - ha a válasz helytelen, akkor az a benyomásunk támad, hogy az illető nem ért egyszerű dolgokat és/vagy nem értette a feladat lényegét. Ezt a pillanatot mindig kordában kell tartani, megoldani bármilyen feladatot a felsőbb matematikában és más tárgyakban is.
Hová tűnt a nagy "en" betű? Elvileg rá lehetne ragasztani a megoldásra, de a rekord lerövidítése érdekében nem tettem. Remélem ezt mindenki megérti, és ugyanaz a megjelölés.
Egy népszerű példa a barkácsoló megoldásra:
2. példa
Keresse meg a vektorokra épített háromszög területét, ha 
A háromszög területének vektorszorzaton keresztüli meghatározásának képlete a definíció megjegyzéseiben található. Megoldás és válasz a lecke végén.
A gyakorlatban a feladat valóban nagyon gyakori, a háromszögeket általában meg lehet kínozni.
Más problémák megoldásához szükségünk van:
A vektorszorzat néhány tulajdonságát már megvizsgáltuk, de ebbe a listába felveszem őket.
Tetszőleges vektorokra és tetszőleges számokra a következő tulajdonságok igazak:
1) Más információforrásokban ezt az elemet általában nem különböztetik meg a tulajdonságokban, de gyakorlati szempontból nagyon fontos. Úgyhogy legyen.
2) 
- fentebb is szó van az ingatlanról, néha ún antikommutativitás. Más szóval, a vektorok sorrendje számít.
3) - kombináció vagy asszociációs vektor szorzat törvényei. Az állandók könnyen kivehetők a vektorszorzat határaiból. Tényleg, mit keresnek ott?
4) - elosztás ill terjesztés vektor szorzat törvényei. Nincs probléma a zárójelek nyitásával sem.
Szemléltetésként vegyünk egy rövid példát:
3. példa
Keresse meg, ha 
Megoldás: Feltétel alapján ismét meg kell találni a vektorszorzat hosszát. Festjük meg miniatűrünket: 
(1) Az asszociatív törvények szerint a vektorszorzat határain túli állandókat kivesszük.
(2) Kivesszük a konstanst a modulból, miközben a modul „megeszi” a mínusz jelet. A hossza nem lehet negatív.
(3) A következők világosak.
Válasz: 
Ideje fát dobni a tűzre:
4. példa
Számítsa ki a vektorokra épített háromszög területét, ha 
Megoldás: Keresse meg egy háromszög területét a képlet segítségével 
. A bökkenő az, hogy a "ce" és a "te" vektorok maguk is vektorok összegeként vannak ábrázolva. Az itt található algoritmus szabványos, és némileg emlékeztet a lecke 3. és 4. példájára. Vektorok pontszorzata. Az egyértelműség kedvéért bontsuk három lépésre:
1) Az első lépésben a vektorszorzatot a vektorszorzaton keresztül fejezzük ki, valójában fejezzük ki a vektort a vektorral. A hosszról még nem esett szó!
(1) Behelyettesítjük a vektorok kifejezéseit.
(2) Distributív törvények segítségével kinyitjuk a zárójeleket a polinomok szorzási szabálya szerint.
(3) Az asszociatív törvények segítségével kivesszük a vektorszorzatokon túli összes állandót. Kevés tapasztalattal a 2. és 3. művelet egyszerre is végrehajtható.
(4) A kellemes tulajdonság miatt az első és az utolsó tag egyenlő nullával (nulla vektor). A második tagban a vektorszorzat antikommutatív tulajdonságát használjuk:
(5) Hasonló kifejezéseket mutatunk be.
Ennek eredményeként kiderült, hogy a vektor egy vektoron keresztül fejeződik ki, amit el kellett érni: 
2) A második lépésben megkeressük a szükséges vektorszorzat hosszát. Ez a művelet hasonló a 3. példához: 
3) Keresse meg a kívánt háromszög területét: 
A megoldás 2-3 lépéseit egy sorba lehetne rendezni.
Válasz:
A vizsgált probléma meglehetősen gyakori a tesztekben, itt van egy példa egy független megoldásra:
5. példa
Keresse meg, ha
Rövid megoldás és válasz a lecke végén. Lássuk, milyen figyelmes voltál az előző példák tanulmányozásakor ;-)
A képlet nagyon egyszerű: a determináns felső sorába írjuk a koordináta vektorokat, a második és harmadik sorba „pakoljuk” a vektorok koordinátáit, és szigorú sorrendben- először a "ve" vektor koordinátái, majd a "double-ve" vektor koordinátái. Ha a vektorokat más sorrendben kell szorozni, akkor a sorokat is fel kell cserélni: 
10. példa
Ellenőrizze, hogy a következő térvektorok kollineárisak-e:
A)
b) 
Megoldás: A teszt a leckében található egyik állításon alapul: ha a vektorok kollineárisak, akkor a keresztszorzatuk nulla (nulla vektor): 
.
a) Keresse meg a vektorszorzatot: 
Tehát a vektorok nem kollineárisak.
b) Keresse meg a vektorszorzatot: 
Válasz: a) nem kollineáris, b)
Itt van talán minden alapvető információ a vektorok vektorszorzatáról.
Ez a szakasz nem lesz túl nagy, mivel kevés probléma adódik a vektorok vegyes szorzatának felhasználásával. Valójában minden a meghatározáson, a geometriai jelentésen és néhány működő képleten fog nyugodni.
A vektorok vegyes szorzata három vektor szorzata:
Így álltak sorba, mint a vonat, és várnak, alig várják, amíg kiszámolják őket.
Először is a definíció és a kép:
Meghatározás: Vegyes termék nem egysíkú vektorok, ebben a sorrendben szedve, nak, nek hívják a paralelepipedon térfogata, ezekre a vektorokra épül, "+" jellel, ha az alap jobb, és "-" jellel, ha a bázis bal.
Csináljuk a rajzot. A számunkra láthatatlan vonalakat szaggatott vonal húzza: 
Merüljünk el a definícióban:
2) Felvett vektorok egy bizonyos sorrendben, vagyis a vektorok permutációja a szorzatban, ahogy sejthető, nem marad következmények nélkül.
3) Mielőtt hozzászólnék a geometriai jelentéshez, megjegyzem a nyilvánvaló tényt: vektorok vegyes szorzata SZÁM: . Az oktatási irodalomban a kialakítás némileg eltérhet, én a vegyes terméket szoktam jelölni, a számítások eredményét pedig "pe" betűvel.
A-priory a kevert termék a paralelepipedon térfogata, vektorokra épített (az ábra piros vektorokkal és fekete vonalakkal van megrajzolva). Azaz a szám megegyezik az adott paralelepipedon térfogatával.
jegyzet : A rajz sematikus.
4) Ne foglalkozzunk ismét az alap és a tér orientációjának fogalmával. A záró rész jelentése az, hogy mínusz jelet lehet adni a kötethez. Leegyszerűsítve a vegyes termék lehet negatív: .
A definícióból közvetlenül következik a vektorokra épített paralelepipedon térfogatának kiszámításának képlete.
Nyilvánvaló, hogy keresztszorzat esetén a vektorok felvételi sorrendje számít, sőt,
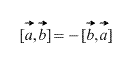
Közvetlenül a definícióból az is következik, hogy bármely k skalártényezőre (szám) igaz a következő:
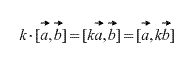
A kollineáris vektorok keresztszorzata egyenlő a nulla vektorral. Ráadásul két vektor keresztszorzata akkor és csak akkor nulla, ha kollineárisak. (Amennyiben az egyik egy nulla vektor, akkor emlékezni kell arra, hogy a nulla vektor definíció szerint kollineáris bármely vektorral).
A vektoros termék rendelkezik elosztó tulajdon, vagyis
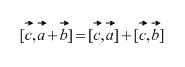
A keresztszorzat kifejezése a vektorok koordinátáiban.
Legyen két vektor adott
(Hogyan lehet megkeresni egy vektor koordinátáit a kezdetének és végének koordinátái alapján – lásd a Vektorok pontszorzata című cikket, A pontszorzat alternatív definíciója, vagy két vektor koordinátáival megadott pontszorzatának kiszámítása című bekezdést.)
Miért van szüksége vektoros termékre?
A keresztszorzat felhasználásának számos módja van, például, ahogy fentebb már írtuk, két vektor keresztszorzatának kiszámításával megtudhatja, hogy kollineárisak-e.
Vagy használható az ezekből a vektorokból épített paralelogramma területének kiszámítására. A definíció alapján a kapott vektor hossza ennek a paralelogrammának a területe.
Ezenkívül számos alkalmazás létezik az elektromosság és a mágnesesség területén.Online számológép vektor termék.
Két vektor skaláris szorzatának meghatározásához ezzel a számológéppel meg kell adni az első vektor koordinátáit az első sorba, és a második vektor koordinátáit a másodikba. A vektorok koordinátái a kezdő- és végkoordinátáikból számíthatók ki (lásd a cikket Vektorok pontszorzata, item A pontszorzat alternatív definíciója, vagy két vektor pontszorzatának kiszámítása a koordinátáik alapján.)
