7.1. Ristkorrutise määratlus
Kolm mittetasatasandilist vektorit a , b ja c võetuna näidatud järjekorras moodustavad parempoolse kolmiku, kui kolmanda vektori c lõpust on näha, et lühim pööre esimesest vektorist a teise vektorisse b on vastupäeva, ja vasak, kui päripäeva (vt joonis . 16).
Vektori a ja vektori b vektorkorrutist nimetatakse vektoriks c, mis:
1. Risti vektoritega a ja b, st c ^ a ja c ^ b;
2. Selle pikkus on arvuliselt võrdne vektoritele a ja ehitatud rööpküliku pindalagab nagu külgedel (vt joon. 17), st.
3. Vektorid a , b ja c moodustavad parempoolse kolmiku.
vektorprodukt tähistatud a x b või [a,b]. Vektorkorrutise definitsioonist tulenevad otseselt järgmised seosed ortide vahel, j Ja k(vt joonis 18):
i x j \u003d k, j x k \u003d i, k x i \u003d j.
Tõestame seda näiteks i xj \u003d k.
1) k ^ i , k ^ j;
2) |k |=1, kuid | i x j| = |i | |J| sin(90°)=1;
3) vektorid i , j ja k moodustavad parempoolse kolmiku (vt joon. 16).
7.2. Risttoodete omadused
1. Tegurite ümberpaigutamisel muudab vektorkorrutis märki, s.t. ja xb \u003d (b xa) (vt joonis 19).
Vektorid a xb ja b xa on kollineaarsed, neil on samad moodulid (rööpküliku pindala jääb muutumatuks), kuid on vastupidise suunaga (vastandsuunalised kolmikud a, b, a xb ja a, b, b x a). See on axb = -(bxa).
2. Vektorkorrutisel on skalaarteguri suhtes kombineeritud omadus, st l (a xb) \u003d (la) x b \u003d a x (l b).
Olgu l >0. Vektor l (a xb) on risti vektoritega a ja b. Vektor ( l a)x b on samuti risti vektoritega a ja b(vektorid a, l kuid lebavad samas tasapinnas). Seega vektorid l(a xb) ja ( l a)x b kollineaarne. On ilmne, et nende suunad langevad kokku. Neil on sama pikkus:
Sellepärast l(a xb)= l a xb. Seda tõestatakse sarnaselt l<0.
3. Kaks nullist erinevat vektorit a ja b on kollineaarsed siis ja ainult siis, kui nende vektorkorrutis on võrdne nullvektoriga, st ja ||b<=>ja xb \u003d 0.
Täpsemalt i *i =j *j =k *k =0 .
4. Vektorkorrutisel on jaotusomadus:
(a+b) xs = a xs + b xs .
Nõustu ilma tõendita.
7.3. Risttoote väljendus koordinaatidena
Kasutame vektorite ristkorrutise tabelit i , j ja k :
kui lühima tee suund esimesest vektorist teise kattub noole suunaga, siis on korrutis võrdne kolmanda vektoriga, kui see ei ühti, võetakse kolmas vektor miinusmärgiga.
Olgu kaks vektorit a =a x i +a y j+az k ja b=bx i+poolt j+bz k. Leiame nende vektorite vektorkorrutise, korrutades need polünoomidena (vastavalt vektorkorrutise omadustele):
Saadud valemi saab kirjutada veelgi lühemalt:
kuna võrdsuse (7.1) parem pool vastab kolmandat järku determinandi laiendusele esimese rea elementide osas Võrdsust (7.2) on lihtne meelde jätta.
7.4. Mõned risttoote rakendused
Vektorite kollineaarsuse tuvastamine
Rööpküliku ja kolmnurga pindala leidmine
Vastavalt vektorite ristkorrutise definitsioonile A ja b |a xb | =| a | * |b |sin g , st S par = |a x b |. Ja seetõttu D S \u003d 1/2 | a x b |.
Jõumomendi määramine punktis
Punkti A rakendatakse jõudu F = AB lase sel minna KOHTA- mingi punkt ruumis (vt joonis 20).
Füüsikast on teada, et pöördemoment F punkti suhtes KOHTA nimetatakse vektoriks M , mis läbib punkti KOHTA Ja:
1) risti punkte läbiva tasapinnaga O, A, B;
2) arvuliselt võrdne jõu ja õla korrutisega
3) moodustab parempoolse kolmiku vektoritega OA ja A B .
Seetõttu M \u003d OA x F.
Lineaarse pöörlemiskiiruse leidmine
Kiirus v nurkkiirusega pöörleva jäiga keha punkt M wümber fikseeritud telje, määratakse Euleri valemiga v \u003d w x r, kus r \u003d OM, kus O on telje mingi fikseeritud punkt (vt joonis 21).
Definitsioon. Vektori a (kordaja) vektorkorrutis vektoriga (kordistiga), mis ei ole tema suhtes kollineaarne, on kolmas vektor c (korrutis), mis konstrueeritakse järgmiselt:
1) selle moodul on arvuliselt võrdne rööpküliku pindalaga joonisel fig. 155), mis on ehitatud vektoritele, st see on võrdne nimetatud rööpküliku tasandiga risti oleva suunaga;
3) sel juhul valitakse vektori c suund (kahest võimalikust) nii, et vektorid c moodustavad parempoolse süsteemi (§ 110).
Nimetus: või
Lisa definitsioonile. Kui vektorid on kollineaarsed, siis vaadeldes joonist (tinglikult) rööpkülikuna, on loomulik määrata nullpindala. Seetõttu loetakse kollineaarsete vektorite vektorkorrutis võrdseks nullvektoriga.
Kuna nullvektorile saab määrata mis tahes suuna, ei ole see konventsioon vastuolus definitsiooni punktidega 2 ja 3.
Märkus 1. Mõistes "vektorkorrutis" näitab esimene sõna, et tegevuse tulemuseks on vektor (erinevalt skalaarkorrutisest; vrd § 104, märkus 1).
Näide 1. Leia vektorkorrutis, kus on õige koordinaatsüsteemi põhivektorid (joonis 156).
1. Kuna põhivektorite pikkused on võrdsed skaalaühikuga, on rööpküliku pindala (ruut) arvuliselt võrdne ühega. Seega on vektorkorrutise moodul võrdne ühega.
2. Kuna tasandiga risti on telg, on soovitud vektorkorrutis vektoriga k kollineaarne vektor; ja kuna mõlemal on moodul 1, on nõutav ristkorrutis kas k või -k.
3. Nendest kahest võimalikust vektorist tuleb valida esimene, kuna vektorid k moodustavad parempoolse süsteemi (ja vektorid moodustavad vasakpoolse).
Näide 2. Leidke ristkorrutis
Lahendus. Nagu näites 1, järeldame, et vektor on kas k või -k. Kuid nüüd peame valima -k, kuna vektorid moodustavad õige süsteemi (ja vektorid moodustavad vasaku). Niisiis,
Näide 3 Vektorite pikkus on vastavalt 80 ja 50 cm ning need moodustavad 30° nurga. Võttes pikkusühikuks meetri, leidke vektorkorrutise a pikkus
Lahendus. Vektoritele ehitatud rööpküliku pindala on võrdne Soovitud vektorkorrutise pikkus on võrdne
Näide 4. Leia samade vektorite ristkorrutise pikkus, võttes pikkuseühikuks sentimeetri.
Lahendus. Kuna vektoritele ehitatud rööpküliku pindala on võrdne vektori korrutise pikkusega, on 2000 cm, s.o.
Näidete 3 ja 4 võrdlus näitab, et vektori pikkus ei sõltu ainult tegurite pikkustest, vaid ka pikkuseühiku valikust.
Vektorkorrutise füüsikaline tähendus. Paljudest vektorkorrutisega esindatud füüsikalistest suurustest võtame arvesse ainult jõumomenti.
Olgu jõu rakenduspunkt A. Jõumomenti punkti O suhtes nimetatakse vektorkorrutiseks. Kuna selle vektorkorrutise moodul on arvuliselt võrdne rööpküliku pindalaga (joonis 157), momendi moodul võrdub aluse korrutisega kõrgusega, st jõu korrutisega kaugusega punktist O kuni sirgjooneni, mida mööda jõud mõjub.
Mehaanikas on tõestatud, et jäiga keha tasakaalu jaoks on vajalik, et mitte ainult kehale rakendatavaid jõude esindavate vektorite summa, vaid ka jõudude momentide summa ei oleks võrdne nulliga. Juhul, kui kõik jõud on paralleelsed sama tasapinnaga, saab momente esindavate vektorite liitmise asendada nende moodulite liitmise ja lahutamisega. Kuid meelevaldsete jõudude suundade puhul on selline asendamine võimatu. Selle kohaselt määratletakse ristkorrutis täpselt vektori, mitte arvuna.
Definitsioon. Vektori a ja vektori b vektorkorrutis on vektor, mida tähistatakse sümboliga [«, b] (või l x b), nii et 1) vektori [a, b] pikkus on võrdne (p, kus y on nurk vektorite a ja b vahel ( 31) 2) vektor [a, b) on risti vektoritega a ja b, s.t. risti nende vektorite tasapinnaga; 3) vektor [a, b] on suunatud nii, et selle vektori lõpust on näha lühimat pööret a-st b-ni vastupäeva (joonis 32). Riis. 32 Joon.31 Teisisõnu, vektorid a, b ja [а, b) moodustavad vektorite parempoolse kolmiku, s.o. paiknevad nagu parema käe pöial, nimetissõrm ja keskmine sõrm. Kui vektorid a ja b on kollineaarsed, siis eeldame, et [a, b] = 0. Definitsiooni järgi on vektori korrutise pikkus arvuliselt võrdne korrutatud vektoritele ehitatud rööpküliku pindalaga Sa (joonis 33). a ja b nagu külgedel: 6.1 . Vektorkorrutise omadused 1. Vektorkorrutis on võrdne nullvektoriga siis ja ainult siis, kui vähemalt üks korrutatud vektoritest on null või kui need vektorid on kollineaarsed (kui vektorid a ja b on kollineaarsed, siis on nendevaheline nurk on kas 0 või 7r). Seda on lihtne saada sellest, et Kui vaadelda nullvektorit kollinaarseks mis tahes vektori suhtes, siis vektorite a ja b kollinaarsuse tingimust saab väljendada järgmiselt 2. Vektorkorrutis on antikommutatiivne, st alati. Tõepoolest, vektorid (a, b) ja on sama pikkusega ja kollineaarsed. Nende vektorite suunad on vastupidised, kuna vektori [a, b] lõpust on näha lühimat pööret a-st b-ni vastupäeva ja vektori [b, a] lõpust päripäeva (joonis 1). 34). 3. Vektorkorrutisel on liitmise 4 suhtes jaotusomadus. Vektorkorrutise märgist 6.2 võib välja võtta arvulise teguri A. Koordinaatidega antud vektorite vektorkorrutis Olgu vektorid a ja b antud nende koordinaatide alusel baasis. Vektorkorrutise jaotusomadust kasutades leiame koordinaatidega antud vektorite vektorkorrutise. Segatööd. Kirjutame välja koordinaatide ortide vektorkorrutised (joonis 35): Seetõttu saame vektorite a ja b vektorkorrutisele valemist (3) järgmise 1. rea elementide avaldise determinandi, saame ( 4). Näited. 1. Leidke vektoritele ehitatud rööpküliku pindala Leidke kolmnurga pindala (joonis 36). On selge, et kolmnurga JSC pindala b "d on võrdne poolega rööpküliku O AC B pindalast S. Vektorkorrutise (a, b | vektorite a \u003d OA ja b \u003d b \u003d ob) arvutamine ), saame (a, b), c) = [a, |b, c)) ei ole üldjuhul tõene Näiteks a = ss j korral on meil § 7. Vektorite segakorrutis Olgu meil kolm vektorit a, b ja c Korrutage vektorid a ja 1> vektoriaalselt Selle tulemusena saame vektori [a, 1>] Korrutame selle skalaarselt vektoriga c: (k b), c Arv ( [a, b], e) nimetatakse vektorite a, b. c segakorrutiseks ja tähistatakse sümboliga (a, 1), e) 7.1. Segakorrutise geomeetriline tähendus Jätame kõrvale vektorid a, b ja üldpunktist O (joon. 37).Kui kõik neli punkti O, A, B, C asuvad samal tasapinnal ( vektoreid a, b ja c nimetatakse sel juhul tasapinnalisteks), siis segatud. korrutis ([a, b], c) = 0. See tuleneb asjaolust, et vektor [a, b| on risti tasapinnaga, millel asuvad vektorid a ja 1 ”, ja seega vektor c. / Kui punktid O, A, B, C ei asu samal tasapinnal (vektorid a, b ja c on mittetasapinnalised), ehitame servadele OA, OB ja OS rööptahuka (joon. 38 a). Ristkorrutise definitsiooni järgi on meil (a,b) = So c, kus So on rööpküliku OADB pindala ja c on ühikvektor, mis on risti vektoritega a ja b ning selline, et kolmik a , b, c on õiged, st. vektorid a, b ja c paiknevad vastavalt parema käe pöidla-, nimetis- ja keskmise sõrmena (joonis 38 b). Korrutades mõlemad viimase võrrandi osad paremal skalaaril vektoriga c, saame, et koordinaatidega antud vektorite vektorkorrutis. Segatööd. Arv rc c on võrdne konstrueeritud rööptahuka kõrgusega h, mis on võetud plussmärgiga, kui vektorite c ja c vaheline nurk on teravnurk (kolmik a, b, c on õige), ja märgiga " -” kui nurk on nüri (kolmik a, b, c - vasak), nii et vektorite a, b ja c segakorrutis on võrdne nendele vektoritele ehitatud rööptahuka ruumalaga V nagu servadele. kui kolmik a, b, c on parem ja -V, kui kolmik a , b, c - vasak. Segakorrutise geomeetrilise tähenduse põhjal võime järeldada, et korrutades samad vektorid a, b ja c mis tahes muus järjekorras, saame alati kas +7 või -K. Märk pro- Joon. 38 viide sõltub ainult sellest, millise tripleti korrutatud vektorid moodustavad - paremale või vasakule. Kui vektorid a, b, c moodustavad parempoolse kolmiku, siis on õiged ka kolmikud b, c, a ja c, a, b. Samal ajal kõik kolm kolmikut b, a, c; a, c, b ja c, b, a - vasakule. Seega (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , A). Rõhutame veel kord, et vektorite segakorrutis on võrdne nulliga siis ja ainult siis, kui korrutatud vektorid a, b, c on tasapinnalised: (a, b, c on tasapinnalised) 7.2. Segakorrutis koordinaatides Olgu vektorid a, b, c antud nende koordinaatidega aluses i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Leiame avaldise nende segakorrutisele (a, b, c). Meil on vektorite segakorrutis, mis on antud nende koordinaatide alusel aluses i, J, k, mis on võrdne kolmandat järku determinandiga, mille read koosnevad vastavalt korrutatud esimese, teise ja kolmanda koordinaatidest. vektorid. Vajaliku ja piisava tingimuse vektorite a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) komplanaarsuseks saab kirjutada järgmisel kujul z, ar2y2-2 =0. Uz Näide. Kontrollige, kas vektorid v = (7,4,6), b = (2, 1,1), c = (19, II, 17) on tasapinnalised. Vaadeldavad vektorid on samatasandilised või mitte-tasapinnalised, olenevalt sellest, kas determinant on võrdne nulliga või mitte. Laiendades seda esimese rea elementide osas, saame 7.3. Topeltkorrutis Topeltristkorrutis [a, [b, c]] on vektor, mis on risti vektoritega a ja [b, c]. Seetõttu asub see vektorite b ja c tasapinnal ning seda saab nendes vektorites laiendada. Saab näidata, et valem [a, [!>, c]] = b(a, e) - c(a, b) kehtib. Ülesanded 1. Kolm vektorit AB = c, W? = o ja CA = b on kolmnurga külgedeks. Väljendage a, b ja c abil vektoreid, mis langevad kokku kolmnurga mediaanidega AM, DN, CP. 2. Milline tingimus peab olema ühendatud vektorite p ja q vahel, et vektor p + q jagaks nendevahelise nurga pooleks? Eeldatakse, et kõik kolm vektorit on seotud ühise päritoluga. 3. Arvutage vektoritele a = 5p + 2q ja b = p - 3q ehitatud rööpküliku diagonaalide pikkus, kui on teada, et |p| = 2v/2, |q| = 3H-(p7ci) = f. 4. Tähistage rombi ühisest tipust väljuvaid külgi a ja b-ga, tõestage, et rombi diagonaalid on üksteisega risti. 5. Arvutage vektorite a = 4i + 7j + 3k ja b = 31 - 5j + k punktkorrutis. 6. Leidke vektoriga a = (6, 7, -6) paralleelne ühikvektor a0. 7. Leidke vektori projektsioon a = l+ j- kHa vektor b = 21 - j - 3k. 8. Leidke vektorite vahelise nurga koosinus IS "w, kui A (-4,0,4), B (-1,6,7), C (1,10,9). 9. Leia ühikvektor p°, mis on samaaegselt risti vektoriga a = (3, 6, 8) ja x-teljega. 10. Arvutage vektoritele a = 2i+J-k, b=i-3j + k nagu külgedel ehitatud rööptahuka diagonaalide vahelise nurga siinus. Arvutage vektoritele a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k ehitatud rööptahuka kõrgus h, kui aluseks võtta vektoritele a ja I ehitatud rööpkülik). Vastused
Selles õppetükis vaatleme veel kahte vektoritega tehtavat toimingut: vektorite ristkorrutis Ja vektorite segakorrutis (vahetu link neile, kes seda vajavad). Pole hullu, vahel juhtub, et täielikuks õnneks lisaks vektorite punktkorrutis, on vaja järjest rohkem. Selline on vektorsõltuvus. Võib jääda mulje, et oleme sattumas analüütilise geomeetria džunglisse. See on vale. Kõrgema matemaatika selles osas on küttepuid üldiselt vähe, välja arvatud ehk piisavalt Pinocchio jaoks. Tegelikult on materjal väga levinud ja lihtne – vaevalt raskem kui sama skalaarkorrutis, isegi tüüpilisi ülesandeid on vähem. Peamine asi analüütilises geomeetrias, nagu paljud näevad või on juba näinud, on MITTE VEDA ARVUTUSTES. Korrake nagu loitsu ja olete õnnelik =)
Kui vektorid sädelevad kusagil kaugel, nagu välk silmapiiril, siis pole vahet, alusta õppetunniga Mannekeenide vektorid taastada või omandada algteadmised vektorite kohta. Ettevalmistumad lugejad saavad infoga tutvuda valikuliselt, püüdsin kokku koguda võimalikult tervikliku näitekogu, mida praktilises töös sageli leidub
Mis teeb sind õnnelikuks? Kui olin väike, oskasin kahe ja isegi kolme palliga žongleerida. See tuli hästi välja. Nüüd pole üldse vaja žongleerida, kuna me kaalume ainult ruumivektorid, ja kahe koordinaadiga lamevektorid jäetakse välja. Miks? Nii need tegevused sündisid – vektor ja vektorite segakorrutis on defineeritud ja toimivad kolmemõõtmelises ruumis. Juba lihtsam!
Selles toimingus, samamoodi nagu skalaarkorrutis, kaks vektorit. Olgu need kadumatud tähed.
Tegevus ise tähistatud järgmisel viisil: . On ka teisi võimalusi, aga ma olen harjunud vektorite ristkorrutist niimoodi tähistama, nurksulgudes koos ristiga.
Ja kohe küsimus: kui sisse vektorite punktkorrutis kaasatud on kaks vektorit ja siin korrutatakse ka kaks vektorit, siis mis vahe on? Selge erinevus, esiteks TULEMUSES:
Vektorite skalaarkorrutise tulemus on ARV:
Vektorite ristkorrutise tulemus on VEKTOR: , ehk siis korrutame vektorid ja saame uuesti vektori. Suletud klubi. Tegelikult sellest ka operatsiooni nimi. Erinevas õppekirjanduses võivad tähistused samuti erineda, kasutan tähte .
Kõigepealt tuleb pildiga definitsioon, seejärel kommentaarid.
Definitsioon: risttoode mittekollineaarne vektorid, võetud selles järjekorras, nimetatakse VECTORiks, pikkus mis on arvuliselt võrdne rööpküliku pindalaga, ehitatud nendele vektoritele; vektor vektoritega ortogonaalne, ja on suunatud nii, et alus oleks õiges suunas: 
Analüüsime definitsiooni luude kaupa, seal on palju huvitavat!
Seega võime esile tõsta järgmisi olulisi punkte:
1) Lähtevektorid, definitsiooni järgi tähistatud punaste nooltega mitte kollineaarne. Kollineaarsete vektorite juhtumit on asjakohane käsitleda veidi hiljem.
2) Võetud vektorid ranges järjekorras: – "a" korrutatakse arvuga "olla", mitte "olema" asemel "a". Vektori korrutamise tulemus on VECTOR , mis on tähistatud sinisega. Kui vektoreid korrutada vastupidises järjekorras, siis saame vektori, mis on võrdne pikkusega ja vastassuunas (karmiinpunane). See tähendab võrdsust 
.
3) Nüüd tutvume vektorkorrutise geomeetrilise tähendusega. See on väga oluline punkt! Sinise vektori (ja seega ka karmiinpunase vektori ) PIKKUS on arvuliselt võrdne vektoritele ehitatud rööpküliku PIIRKONNAga. Joonisel on see rööpkülik mustaks varjutatud.
Märge : joonis on skemaatiline ja loomulikult ei võrdu ristkorrutise nimipikkus rööpküliku pindalaga.
Tuletame meelde ühte geomeetrilistest valemitest: rööpküliku pindala on võrdne külgnevate külgede ja nendevahelise nurga siinuse korrutisega. Seetõttu kehtib eelneva põhjal vektorkorrutise PIKKUSE arvutamise valem:
Rõhutan, et valemis räägime vektori PIKKUSEST, mitte vektorist endast. Mis on praktiline tähendus? Ja tähendus on selline, et analüütilise geomeetria probleemide korral leitakse rööpküliku pindala sageli vektorkorrutise kontseptsiooni kaudu:
Saame teise olulise valemi. Rööpküliku diagonaal (punane punktiirjoon) jagab selle kaheks võrdseks kolmnurgaks. Seetõttu saab vektoritele ehitatud kolmnurga pindala (punane varjutus) leida valemiga:
4) Sama oluline fakt on see, et vektor on vektoritega ortogonaalne, see tähendab 
. Muidugi on ka vastupidise suunaga vektor (karmiinpunane nool) ortogonaalne algsete vektoritega .
5) Vektor on suunatud nii alus Sellel on õige orientatsiooni. Õppetunnis umbes üleminek uuele alusele Olen sellest üksikasjalikult rääkinud tasapinnaline orientatsioon, ja nüüd selgitame välja, mis on ruumi orientatsioon. Ma selgitan teile sõrmedel parem käsi. Vaimselt kombineerida nimetissõrm vektoriga ja keskmine sõrm vektoriga. Sõrmuse sõrm ja väike sõrm suruge peopessa. Tulemusena pöial- vektorkorrutis otsib üles. See on paremale suunatud alus (see on joonisel). Nüüd vaheta vektorid ( nimetis- ja keskmised sõrmed) mõnes kohas pöördub selle tulemusena pöial ümber ja vektorkorrutis vaatab juba alla. See on ka paremale suunatud alus. Võib-olla on teil küsimus: mis alusel on vasakpoolne orientatsioon? "Määrake" samad sõrmed vasak käsi vektorid ja saate vasakpoolse baasi ja vasakpoolse ruumi orientatsiooni (sel juhul asub pöial alumise vektori suunas). Piltlikult öeldes “väänavad” või orienteerivad need alused ruumi eri suundades. Ja seda kontseptsiooni ei tohiks pidada millekski kaugeks või abstraktseks - näiteks muudab kõige tavalisem peegel ruumi orientatsiooni ja kui "tõmbate peegeldunud objekti peeglist välja", siis üldiselt pole see võimalik ühendage see "originaaliga". Muide, tooge kolm sõrme peegli juurde ja analüüsige peegeldust ;-)
... kui hea on see, et sa sellest nüüd tead paremale ja vasakule orienteeritud alused, sest osade õppejõudude väited orientatsiooni muutumise kohta on kohutavad =)
Definitsioon on üksikasjalikult välja töötatud, jääb üle välja selgitada, mis juhtub, kui vektorid on kollineaarsed. Kui vektorid on kollineaarsed, siis saab need asetada ühele sirgele ja ka meie rööpkülik “voldib” üheks sirgeks. Selliste ala, nagu matemaatikud ütlevad, degenereerunud rööpkülik on null. Sama tuleneb valemist - nulli ehk 180 kraadi siinus võrdub nulliga, mis tähendab, et pindala on null
Seega, kui , siis 
Ja 
. Pange tähele, et ristkorrutis ise on võrdne nullvektoriga, kuid praktikas jäetakse see sageli tähelepanuta ja kirjutatakse, et see on samuti võrdne nulliga.
Erijuhtum on vektori ja enda vektorkorrutis:
Ristkorrutist kasutades saab kontrollida kolmemõõtmeliste vektorite kollineaarsust ning analüüsime muuhulgas ka seda probleemi.
Praktiliste näidete lahendamiseks võib see osutuda vajalikuks trigonomeetriline tabel siit siinuste väärtuste leidmiseks.
Noh, teeme tuld:
Näide 1
a) Leia vektorite vektorkorrutise pikkus, kui 
b) Leidke vektoritele ehitatud rööpküliku pindala, kui 
Lahendus: Ei, see pole kirjaviga, muutsin tingimuse üksuste lähteandmed tahtlikult samaks. Sest lahenduste kujundus on erinev!
a) Vastavalt tingimusele on vaja leida pikkus vektor (vektori korrutis). Vastavalt vastavale valemile:
Vastus:
Kuna küsiti pikkuse kohta, siis vastuses märgime mõõtme - ühikud.
b) Vastavalt tingimusele on vaja leida ruut vektoritele ehitatud rööpkülik . Selle rööpküliku pindala on arvuliselt võrdne ristkorrutise pikkusega:
Vastus:
Pange tähele, et vektorkorrutise vastuses pole üldse juttu, meilt küsiti selle kohta figuuri piirkond, mõõde on vastavalt ruutühikud.
Vaatame alati, MIDA tingimus peab leidma, ja selle põhjal sõnastame selge vastama. See võib tunduda sõnasõnalisusena, kuid õpetajate hulgas on piisavalt literaliste ja suure tõenäosusega ülesanne tagastatakse ülevaatamiseks. Kuigi tegemist ei ole eriti pingutatud näpunäidetega – kui vastus on vale, siis jääb mulje, et inimene ei saa lihtsatest asjadest aru ja/või pole ülesande olemusest aru saanud. Seda hetke tuleks alati kontrolli all hoida, lahendades mis tahes ülesandeid kõrgemas matemaatikas ja ka teistes ainetes.
Kuhu kadus suur "en" täht? Põhimõtteliselt võiks selle täiendavalt lahenduse külge kinni jääda, aga rekordi lühendamiseks ma seda ei teinud. Loodan, et kõik saavad sellest aru ja tähistavad sama asja.
Populaarne näide isetegemise lahendusest:
Näide 2
Leidke vektoritele ehitatud kolmnurga pindala, kui 
Vektorkorrutise kaudu kolmnurga pindala leidmise valem on toodud definitsiooni kommentaarides. Lahendus ja vastus tunni lõpus.
Praktikas on ülesanne tõesti väga levinud, kolmnurki saab üldiselt piinata.
Muude probleemide lahendamiseks vajame:
Oleme juba vaaginud mõnda vektorprodukti omadust, kuid lisan need sellesse loendisse.
Suvaliste vektorite ja suvalise arvu korral kehtivad järgmised omadused:
1) Teistes teabeallikates seda elementi omadustes tavaliselt ei eristata, kuid see on praktilises mõttes väga oluline. Nii et las olla.
2) 
- vara on ka ülalpool juttu, vahel nimetatakse antikommutatiivsus. Teisisõnu, vektorite järjekord on oluline.
3) - kombinatsioon või assotsiatiivne vektorkorrutise seadused. Konstandid on kergesti eemaldatavad vektorkorrutise piiridest. Tõesti, mida nad seal teevad?
4) - levitamine või levitamine vektorkorrutise seadused. Ka sulgude avamisega pole probleeme.
Näitena kaaluge lühikest näidet:
Näide 3
Leia, kui 
Lahendus: Tingimuse järgi on jällegi vaja leida vektorkorrutise pikkus. Maalime oma miniatuuri: 
(1) Vastavalt assotsiatiivsetele seadustele võtame konstandid välja vektorkorrutise piiridest.
(2) Me võtame moodulist välja konstandi, samal ajal kui moodul “sööb” miinusmärgi. Pikkus ei saa olla negatiivne.
(3) Järgnev on selge.
Vastus: 
On aeg puid tulle visata:
Näide 4
Arvutage vektoritele ehitatud kolmnurga pindala, kui 
Lahendus: leidke valemi abil kolmnurga pindala 
. Probleem seisneb selles, et vektorid "ce" ja "te" on ise esitatud vektorite summadena. Siinne algoritm on standardne ja meenutab mõneti tunni näiteid nr 3 ja 4. Vektorite punktkorrutis. Selguse huvides jagame selle kolmeks etapiks:
1) Esimeses etapis väljendame vektorprodukti vektorkorrutise kaudu, tegelikult väljendada vektorit vektori kaudu. Pikkuse kohta pole veel sõnagi!
(1) Asendame vektorite avaldised.
(2) Kasutades distributsiooniseadusi, avame sulud polünoomide korrutamise reegli järgi.
(3) Kasutades assotsiatiivseid seadusi, võtame välja kõik konstandid väljaspool vektorkorrutisi. Vähese kogemuse korral saab toiminguid 2 ja 3 teha samaaegselt.
(4) Esimene ja viimane liige on meeldiva omaduse tõttu võrdsed nulliga (nullvektor). Teises terminis kasutame vektori korrutise antikommutatiivsuse omadust:
(5) Esitame sarnased terminid.
Selle tulemusel selgus, et vektor oli väljendatud vektori kaudu, mis oli see, mida oli vaja saavutada: 
2) Teises etapis leiame meile vajaliku vektorkorrutise pikkuse. See toiming sarnaneb näitega 3: 
3) Leidke soovitud kolmnurga pindala: 
Lahenduse etapid 2-3 võiks olla paigutatud ühele reale.
Vastus:
Vaadeldav probleem on testides üsna tavaline, siin on näide iseseisva lahenduse jaoks:
Näide 5
Leia, kui
Lühilahendus ja vastus tunni lõpus. Vaatame, kui tähelepanelik sa eelmisi näiteid uurides olid ;-)
Valem on tõesti lihtne: determinandi ülemisele reale kirjutame koordinaatvektorid, teisele ja kolmandale reale “pakime” vektorite koordinaadid ja paneme ranges järjekorras- esiteks vektori "ve" koordinaadid, seejärel vektori "double-ve" koordinaadid. Kui vektoreid on vaja korrutada teises järjekorras, tuleb ka read vahetada: 
Näide 10
Kontrollige, kas järgmised ruumivektorid on kollineaarsed:
A)
b) 
Lahendus: Test põhineb ühel selle õppetunni väitel: kui vektorid on kollineaarsed, siis on nende ristkorrutis null (nullvektor): 
.
a) Leidke vektorkorrutis: 
Seega ei ole vektorid kollineaarsed.
b) Leidke vektorkorrutis: 
Vastus a) mitte kollineaarne, b)
Siin on võib-olla kogu põhiteave vektorite vektorkorrutise kohta.
See jaotis ei ole väga suur, kuna vektorite segakorrutise kasutamisel on vähe probleeme. Tegelikult toetub kõik määratlusele, geomeetrilisele tähendusele ja paarile töövalemile.
Vektorite segakorrutis on kolme vektori korrutis:
Nii rivistusid nad nagu rong ja ootavad, nad ei jõua ära oodata, kuni välja arvutatakse.
Kõigepealt jälle definitsioon ja pilt:
Definitsioon: Segatoode mitte-tasapinnaline vektorid, võetud selles järjekorras, kutsutakse rööptahuka maht, mis on ehitatud nendele vektoritele, varustatud märgiga "+", kui alus on õige, ja märgiga "-", kui alus on vasakpoolne.
Teeme joonistamise. Meile nähtamatud jooned on joonistatud punktiirjoonega: 
Sukeldume määratlusse:
2) Võetud vektorid kindlas järjekorras, see tähendab, et vektorite permutatsioon korrutises, nagu võite arvata, ei jää tagajärgedeta.
3) Enne geomeetrilise tähenduse kommenteerimist märgin ära ilmse fakti: vektorite segakorrutis on ARV: . Õppekirjanduses võib kujundus olla mõnevõrra erinev, varem tähistasin segatoodet läbi ja arvutuste tulemust tähega "pe".
A-prioor segaprodukt on rööptahuka ruumala, ehitatud vektoritele (joonis on joonistatud punaste vektorite ja mustade joontega). See tähendab, et arv on võrdne antud rööptahuka helitugevusega.
Märge : Joonis on skemaatiline.
4) Ärme hakka jälle vaeva nägema aluse ja ruumi orientatsiooni mõistega. Lõpuosa tähendus on see, et helitugevusele saab lisada miinusmärgi. Lihtsamalt öeldes võib segatoode olla negatiivne: .
Definitsioonist tuleneb otseselt vektoritele ehitatud rööptahuka ruumala arvutamise valem.
Ilmselgelt on ristkorrutise puhul oluline vektorite võtmise järjekord, pealegi
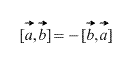
Samuti tuleneb definitsioonist otse, et mis tahes skalaarteguri k (arv) puhul kehtib järgmine:
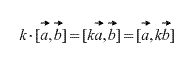
Kollineaarsete vektorite ristkorrutis on võrdne nullvektoriga. Pealegi on kahe vektori ristkorrutis null siis ja ainult siis, kui need on kollineaarsed. (Juhul kui üks neist on nullvektor, tuleb meeles pidada, et nullvektor on definitsiooni järgi mis tahes vektoriga kollineaarne).
Vektortootel on jaotusvara, see on
Ristkorrutise avaldis vektorite koordinaatidena.
Olgu antud kaks vektorit
(kuidas leida vektori koordinaate selle alguse ja lõpu koordinaatide järgi – vaata artiklit Vektorite punktkorrutis, lõik Punktkorrutise alternatiivne määratlus ehk kahe vektori punktkorrutise arvutamine nende koordinaatide järgi.)
Miks on vaja vektortoodet?
Ristkorrutise kasutamiseks on palju võimalusi, näiteks, nagu juba eespool kirjutatud, saab kahe vektori ristkorrutise arvutamisel teada, kas need on kollineaarsed.
Või saab seda kasutada nendest vektoritest koostatud rööpküliku pindala arvutamiseks. Definitsiooni põhjal on saadud vektori pikkus selle rööpküliku pindala.
Samuti on elektri ja magnetismi valdkonnas palju rakendusi.Vektorprodukti veebikalkulaator.
Selle kalkulaatori abil kahe vektori skalaarkorrutise leidmiseks peate esimesele reale sisestama esimese vektori koordinaadid ja teisele teise vektori koordinaadid. Vektorite koordinaate saab arvutada nende algus- ja lõppkoordinaatide järgi (vt artiklit Vektorite punktkorrutis , üksus Punktkorrutise alternatiivne määratlus või kahe vektori punktkorrutise arvutamine nende koordinaatide alusel.)
