डॉट उत्पाद गुण
वैक्टर, परिभाषा, गुणों का डॉट उत्पाद
वैक्टर पर रैखिक संचालन।
वेक्टर, बुनियादी अवधारणाएं, परिभाषाएं, उन पर रैखिक संचालन
एक समतल पर एक सदिश उसके बिंदुओं का एक क्रमित युग्म होता है, जबकि पहले बिंदु को शुरुआत कहा जाता है, और दूसरा अंत - सदिश का
दो वैक्टर समान कहलाते हैं यदि वे समान और कोडायरेक्शनल हैं।
वे सदिश जो एक ही रेखा पर स्थित होते हैं, उन्हें कोडायरेक्शनल कहा जाता है यदि वे उसी सदिश में से कुछ के साथ कोडायरेक्शनल होते हैं जो इस रेखा पर स्थित नहीं होते हैं।
वे सदिश जो एक ही रेखा या समानांतर रेखाओं पर स्थित होते हैं, संरेख कहलाते हैं, और संरेखक, लेकिन कोडायरेक्शनल नहीं, विपरीत दिशा वाले कहलाते हैं।
लंब रेखाओं पर स्थित वैक्टर को ऑर्थोगोनल कहा जाता है।
परिभाषा 5.4. जोड़ क+ख वैक्टर ए और बी वेक्टर की शुरुआत से आने वाला वेक्टर कहा जाता है ए वेक्टर के अंत तक बी , यदि वेक्टर की शुरुआत बी वेक्टर के अंत के साथ मेल खाता है ए .
परिभाषा 5.5. अंतर ए - बी वैक्टर ए और बी ऐसा वेक्टर कहा जाता है साथ , जो एक साथ वेक्टर के साथ बी एक वेक्टर देता है ए .
परिभाषा 5.6। कामक ए वेक्टर ए प्रति संख्या कवेक्टर कहा जाता है बी , संरेख वेक्टर ए , जिसका मॉड्यूल | के बराबर है क||ए |, और एक दिशा जो दिशा के समान है ए पर क> 0 और विपरीत ए पर क<0.
किसी सदिश को किसी संख्या से गुणा करने के गुण:
संपत्ति 1. क(क+ख ) = के ए+ के बी.
संपत्ति 2. (के+एम)ए = के ए+ म ए.
संपत्ति 3। के (एम ए) = (किमी)ए .
परिणाम। यदि गैर-शून्य वैक्टर ए और बी संरेख हैं, तो एक संख्या है क, क्या ख = क ए.
दो शून्येतर सदिशों का अदिश गुणनफल एऔर बीइन सदिशों की लंबाई और उनके बीच के कोण φ के गुणनफल के बराबर एक संख्या (अदिश) कहलाती है। स्केलर उत्पाद को विभिन्न तरीकों से व्यक्त किया जा सकता है, उदाहरण के लिए, जैसे अब, ए · बी, (ए , बी), (ए · बी). तो डॉट उत्पाद है:
ए · बी = |ए| · | बी| क्योंकि φ
यदि सदिशों में से कम से कम एक शून्य के बराबर है, तो अदिश गुणनफल शून्य के बराबर होता है।
क्रमचय संपत्ति: ए · बी = बी · ए(कारकों के क्रमचय से अदिश गुणनफल नहीं बदलता);
वितरण संपत्ति: ए · ( बी · सी) = (ए · बी) · सी(परिणाम गुणन के क्रम पर निर्भर नहीं करता है);
संयोजन संपत्ति (अदिश कारक के संबंध में): (λ ए) · बी = λ ( ए · बी).
ऑर्थोगोनलिटी (लंबवत) की संपत्ति: यदि वेक्टर एऔर बीगैर-शून्य, तब उनका डॉट उत्पाद शून्य होता है जब ये वैक्टर ऑर्थोगोनल (एक दूसरे के लंबवत) होते हैं ए ┴ बी;
स्क्वायर संपत्ति: ए · ए = ए 2 = |ए| 2 (स्वयं सदिश का अदिश गुणनफल इसके मापांक के वर्ग के बराबर होता है);
यदि सदिशों के निर्देशांक ए=(x 1 , y 1 , z 1 ) और बी=(x 2 , y 2 , z 2 ), तो अदिश गुणनफल है ए · बी= x 1 x 2 + y 1 y 2 + z 1 z 2।
वेक्टर होल्डिंग वैक्टर। परिभाषा: दो वैक्टरों का वेक्टर उत्पाद और एक वेक्टर के रूप में समझा जाता है जिसके लिए:
मॉड्यूल इन सदिशों पर निर्मित समांतर चतुर्भुज के क्षेत्रफल के बराबर होता है, अर्थात , जहां वैक्टर और के बीच का कोण है
यह सदिश गुणित सदिशों के लंबवत है, अर्थात
यदि सदिश असंरेख हैं, तो वे सदिशों का एक सही त्रिक बनाते हैं।
क्रॉस उत्पाद गुण:
1. जब कारकों का क्रम बदल जाता है, तो वेक्टर उत्पाद मॉड्यूल को संरक्षित करते हुए, विपरीत दिशा में अपना संकेत बदलता है, अर्थात।
2 .वेक्टर वर्ग शून्य-वेक्टर के बराबर है, अर्थात
3 सदिश गुणनफल के चिह्न से अदिश कारक को निकाला जा सकता है, अर्थात
4 किन्हीं तीन सदिशों के लिए, समानता
5 दो सदिशों की संरेखता के लिए आवश्यक और पर्याप्त स्थिति और :
परिभाषा। वेक्टर ए और वेक्टर बी का वेक्टर उत्पाद प्रतीक [«, बी] (या एल एक्स बी) द्वारा चिह्नित वेक्टर है, जैसे कि 1) वेक्टर की लंबाई [ए, बी] बराबर है (पी, जहां वाई है वैक्टर ए और बी (31) के बीच का कोण; 2) वेक्टर [ए, बी) वैक्टर ए और बी के लिए लंबवत है, अर्थात। इन सदिशों के तल के लंबवत; 3) वेक्टर [ए, बी] को इस तरह से निर्देशित किया जाता है कि इस वेक्टर के अंत से ए से बी तक का सबसे छोटा मोड़ वामावर्त होता है (चित्र 32)। चावल। 32 चित्र 31 दूसरे शब्दों में, सदिश a, b और [а, b) सदिशों का सही त्रिक बनाते हैं, अर्थात दाहिने हाथ के अंगूठे, तर्जनी और मध्यमा की तरह स्थित है। यदि वेक्टर ए और बी कॉललाइनर हैं, तो हम मान लेंगे कि [ए, बी] = 0. परिभाषा के अनुसार, वेक्टर उत्पाद की लंबाई संख्यात्मक रूप से समांतर चतुर्भुज (छवि 33) के क्षेत्रफल के बराबर है, जो गुणित वैक्टर पर निर्मित है। ए और बी पक्षों के रूप में: 6.1। एक सदिश उत्पाद के गुण 1. एक सदिश उत्पाद एक शून्य सदिश के बराबर होता है यदि और केवल यदि गुणित सदिशों में से कम से कम एक शून्य हो या जब ये सदिश समरेख हों (यदि सदिश a और b संरेख हैं, तो उनके बीच का कोण या तो 0 या 7r है)। यह इस तथ्य से प्राप्त करना आसान है कि यदि हम शून्य वेक्टर कोलिन्सर को किसी भी वेक्टर पर विचार करते हैं, तो वैक्टर ए और बी की संपार्श्विकता की स्थिति को निम्नानुसार व्यक्त किया जा सकता है। वेक्टर उत्पाद एंटीकोम्यूटेटिव है, अर्थात हमेशा। दरअसल, वैक्टर (ए, बी) और एक ही लंबाई है और समरेख हैं। इन वैक्टरों की दिशाएं विपरीत हैं, क्योंकि वेक्टर के अंत से [ए, बी] ए से बी तक का सबसे छोटा मोड़ वामावर्त होता हुआ दिखाई देगा, और वेक्टर के अंत से [बी, ए] - दक्षिणावर्त (चित्र। 34). 3. वेक्टर उत्पाद में अतिरिक्त 4 के संबंध में एक वितरण गुण है। संख्यात्मक कारक A को वेक्टर उत्पाद 6.2 के चिन्ह से बाहर निकाला जा सकता है। निर्देशांकों द्वारा दिए गए सदिशों के सदिश गुणनफल मान लीजिए सदिशों a और b को उनके निर्देशांकों के आधार पर दिया गया है। वेक्टर उत्पाद के वितरण गुण का उपयोग करते हुए, हम निर्देशांक द्वारा दिए गए वैक्टर के वेक्टर उत्पाद का पता लगाते हैं। मिश्रित कार्य। आइए हम निर्देशांक ऑर्ट्स (चित्र 35) के वेक्टर उत्पादों को लिखें: इसलिए, वैक्टर ए और बी के वेक्टर उत्पाद के लिए, हम सूत्र (3) से प्राप्त करते हैं, पहली पंक्ति के तत्वों पर निम्नलिखित अभिव्यक्ति निर्धारक, हम प्राप्त करते हैं ( 4). उदाहरण। 1. सदिशों पर निर्मित समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए त्रिभुज का क्षेत्रफल ज्ञात कीजिए (चित्र 36)। यह स्पष्ट है कि त्रिभुज JSC का क्षेत्र b "d समांतर चतुर्भुज O AC B के आधे क्षेत्र S के बराबर है। वेक्टर उत्पाद (a, b | वैक्टर a \u003d OA और b \u003d b \u003d ob) की गणना करना ), हम प्राप्त करते हैं (a, b), c) = [a, |b, c)) सामान्य स्थिति में सत्य नहीं है। उदाहरण के लिए, a = ss j के लिए हमारे पास § 7 है। सदिशों का मिश्रित गुणनफल आइए हम पाते हैं तीन वैक्टर ए, बी और सी। वैक्टर ए और 1> सदिश रूप से गुणा करें। नतीजतन, हम वेक्टर [ए, 1>] प्राप्त करते हैं। हम इसे सदिश सी: (के बी), सी द्वारा स्केलरली गुणा करते हैं। संख्या ( [ए, बी], ई) को वैक्टर ए, बी। सी का मिश्रित उत्पाद कहा जाता है और इसे प्रतीक (ए, 1), ई द्वारा निरूपित किया जाता है। 7.1। मिश्रित उत्पाद का ज्यामितीय अर्थ आइए हम अलग सेट करें वैक्टर ए, बी और सामान्य बिंदु ओ (चित्र 37) से। यदि सभी चार बिंदु ओ, ए, बी, सी एक ही विमान में स्थित हैं (वैक्टर ए, बी और सी को इस मामले में समतलीय कहा जाता है), तो मिश्रित उत्पाद ([ए, बी], सी) = 0। यह इस तथ्य से अनुसरण करता है कि वेक्टर [ए, बी | उस विमान के लंबवत है जिसमें वैक्टर ए और 1 झूठ ", और इसलिए वेक्टर सी। / यदि टी बिंदु O, A, B, C एक ही तल में स्थित नहीं हैं (वैक्टर a, b और c गैर-समतलीय हैं), हम किनारों OA, OB और OS पर एक समानांतर चतुर्भुज का निर्माण करेंगे (चित्र। 38 ए)। क्रॉस उत्पाद की परिभाषा के अनुसार, हमारे पास (ए, बी) = तो सी है, जहां समांतरोग्राम ओएडीबी का क्षेत्र है, और सी वैक्टर ए और बी के लिए एक इकाई वेक्टर लंबवत है और इस तरह ट्रिपल ए , बी, सी सही है, यानी वैक्टर ए, बी और सी क्रमशः दाहिने हाथ के अंगूठे, तर्जनी और मध्य उंगलियों के रूप में स्थित हैं (चित्र 38 बी)। पिछले समानता के दोनों हिस्सों को सदिश c द्वारा सही स्केलर पर गुणा करने पर, हम निर्देशांक द्वारा दिए गए सदिशों के सदिश गुणनफल को प्राप्त करते हैं। मिश्रित कार्य। संख्या आरसी सी निर्मित समांतर चतुर्भुज की ऊंचाई एच के बराबर है, जिसे "+" चिह्न के साथ लिया जाता है यदि वैक्टर सी और सी के बीच का कोण तीव्र है (ट्रिपल ए, बी, सी सही है), और चिह्न के साथ " -" यदि कोण अधिक है (ट्रिपल ए, बी, सी - बाएं), ताकि इस प्रकार, वैक्टर ए, बी और सी का मिश्रित उत्पाद किनारों पर इन वैक्टरों पर निर्मित समांतर चतुर्भुज के आयतन V के बराबर हो अगर ट्रिपल ए, बी, सी सही है, और -वी अगर ट्रिपल ए, बी, सी - बाएं। मिश्रित उत्पाद के ज्यामितीय अर्थ के आधार पर, हम यह निष्कर्ष निकाल सकते हैं कि किसी अन्य क्रम में एक ही वैक्टर ए, बी और सी को गुणा करके, हम हमेशा +7 या -के प्राप्त करेंगे। प्रो-अंजीर का संकेत। 38 संदर्भ केवल इस बात पर निर्भर करेगा कि गुणित सदिश किस त्रिक से बनते हैं - दाएँ या बाएँ। यदि सदिश a, b, c एक सम त्रिक बनाते हैं, तो त्रिक b, c, a और c, a, b भी सही होंगे। एक ही समय में, तीनों ट्रिपल बी, ए, सी; ए, सी, बी और सी, बी, ए - बाएं। इस प्रकार, (ए, बी, सी) = (बी, सी, ए) = (सी, ए, बी) = - (बी, ए, सी) = - (ए, सी, बी) = - (सी, बी, ए)। हम एक बार फिर जोर देते हैं कि सदिशों का मिश्रित उत्पाद शून्य के बराबर होता है यदि और केवल यदि गुणित सदिश a, b, c समतलीय हों: (a, b, c समतलीय हैं) 7.2। निर्देशांक में मिश्रित उत्पाद वैक्टर ए, बी, सी को उनके निर्देशांक द्वारा i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c के आधार पर दिया जाता है। = (x3, उज़, 23)। आइए हम उनके मिश्रित उत्पाद (ए, बी, सी) के लिए एक व्यंजक खोजें। हमारे पास i, J, k के आधार पर उनके निर्देशांक द्वारा दिए गए वैक्टरों का एक मिश्रित उत्पाद है, जो तीसरे क्रम के निर्धारक के बराबर है, जिसकी पंक्तियाँ क्रमशः पहले, दूसरे और तीसरे के निर्देशांक से बनी हैं। वैक्टर। सदिशों a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) की समरूपता के लिए आवश्यक और पर्याप्त स्थिति को निम्न रूप में लिखा जा सकता है z, ar2 y2 -2 = 0। उज़ उदाहरण। जाँच करें कि क्या सदिश v = (7,4,6), b = (2, 1,1), c = (19, II, 17) समतलीय हैं। निर्धारक शून्य के बराबर है या नहीं, इस पर निर्भर करते हुए, विचाराधीन वैक्टर समतलीय या गैर समतलीय होंगे। पहली पंक्ति के तत्वों के संदर्भ में इसका विस्तार करते हुए, हम प्राप्त करते हैं 7.3। डबल क्रॉस उत्पाद डबल क्रॉस उत्पाद [ए, [बी, सी]] वैक्टर ए और [बी, सी] के लिए लंबवत एक वेक्टर है। इसलिए, यह वैक्टर b और c के तल में स्थित है और इन वैक्टरों में इसका विस्तार किया जा सकता है। यह दिखाया जा सकता है कि सूत्र [a, [!>, c]] = b(a, e) - c(a, b) मान्य है। अभ्यास 1. तीन सदिश AB = c, W? = o और CA = b त्रिभुज की भुजाओं के रूप में काम करते हैं। त्रिभुज की माध्यिकाओं AM, DN, CP से मेल खाने वाले सदिशों को a, b और c के पदों में व्यक्त कीजिए। 2. सदिशों p और q के बीच किस स्थिति को जोड़ा जाना चाहिए ताकि सदिश p + q उनके बीच के कोण को आधे में विभाजित कर दे? यह माना जाता है कि तीनों वैक्टर एक ही मूल से संबंधित हैं। 3. सदिशों a = 5p + 2q और b = p - 3q पर निर्मित समांतर चतुर्भुज के विकर्णों की लंबाई की गणना करें, यदि यह ज्ञात है कि |p| = 2v/2, |q| = 3 एच-(p7ci) = च। 4. उभयनिष्ठ शीर्ष से निकलने वाले समचतुर्भुज की भुजाओं को a और b से नकारते हुए सिद्ध कीजिए कि समचतुर्भुज के विकर्ण परस्पर लंब हैं। 5. सदिशों a = 4i + 7j + 3k और b = 31 - 5j + k के डॉट उत्पाद की गणना करें। 6. सदिश a = (6, 7, -6) के समांतर इकाई सदिश a0 ज्ञात कीजिए। 7. सदिश a = l+ j- kHa सदिश b = 21 - j - 3k का प्रक्षेपण ज्ञात कीजिए। 8. सदिशों IS "w, यदि A (-4.0.4), B (-1.6.7), C (1.10.9) के बीच कोण का कोज्या ज्ञात कीजिए। 9. एक इकाई सदिश p° ज्ञात कीजिए जो एक साथ सदिश a = (3, 6, 8) और x-अक्ष के लंबवत है। 10. सदिशों a = 2i+J-k, b=i-3j + k पर निर्मित समान्तर चतुर्भुज के विकर्णों के बीच के कोण की ज्या की गणना करें। वैक्टर a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k पर निर्मित समांतर चतुर्भुज की ऊँचाई h की गणना करें, यदि वैक्टर a और I पर बने समानांतर चतुर्भुज को आधार के रूप में लिया जाता है)। जवाब
वैक्टर के बीच का कोण
हमारे लिए दो वैक्टरों के क्रॉस उत्पाद की अवधारणा को पेश करने के लिए, हमें पहले इन वैक्टरों के बीच के कोण जैसी अवधारणा से निपटना होगा।
हमें दो वैक्टर $\overline(α)$ और $\overline(β)$ दिए जाएं। आइए हम अंतरिक्ष में कुछ बिंदु $O$ लेते हैं और वैक्टर $\overline(α)=\overline(OA)$ और $\overline(β)=\overline(OB)$ को इससे अलग करते हैं, फिर कोण $AOB $ को इन वैक्टरों के बीच का कोण कहा जाएगा (चित्र 1)।
संकेतन: $∠(\overline(α),\overline(β))$
परिभाषा 1
दो वैक्टरों का वेक्टर उत्पाद दोनों दिए गए वैक्टरों के लिए एक लंबवत वेक्टर है, और इसकी लंबाई इन वैक्टरों की लंबाई के उत्पाद के बराबर होगी, इन वैक्टरों के बीच कोण की साइन के साथ, और इस वेक्टर में दो प्रारंभिक वाले समान हैं कार्टेशियन समन्वय प्रणाली के रूप में अभिविन्यास।
नोटेशन: $\overline(α)х\overline(β)$।
गणितीय रूप से ऐसा दिखता है:
जाहिर है, वैक्टर का बाहरी उत्पाद दो मामलों में शून्य वेक्टर के बराबर होगा:
स्पष्ट रूप से देखने के लिए कि सदिशों का क्रॉस उत्पाद कैसे पाया जाता है, निम्नलिखित समाधान उदाहरणों पर विचार करें।
उदाहरण 1
वेक्टर $\overline(δ)$ की लंबाई ज्ञात करें, जो निर्देशांक $\overline(α)=(0,4,0)$ और $\overline(β) के साथ वैक्टर के क्रॉस उत्पाद का परिणाम होगा। =(3,0,0 )$।
समाधान.
आइए इन वैक्टरों को कार्टेशियन समन्वय स्थान (चित्र 3) में चित्रित करें:
चित्रा 3. कार्टेशियन समन्वय अंतरिक्ष में वैक्टर। लेखक24 - छात्र पत्रों का ऑनलाइन आदान-प्रदान
हम देखते हैं कि ये वैक्टर क्रमशः ऑक्स और ओए कुल्हाड़ियों पर स्थित हैं। इसलिए, उनके बीच का कोण $90^\circ$ के बराबर होगा। आइए इन सदिशों की लंबाई ज्ञात करें:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
फिर, परिभाषा 1 के अनुसार, हमें मॉड्यूल $|\overline(δ)|$ प्राप्त होता है
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
उत्तर: $12$।
परिभाषा 1 तुरंत दो वैक्टरों के क्रॉस उत्पाद को खोजने का एक तरीका बताता है। चूंकि एक सदिश, एक मूल्य के अतिरिक्त, एक दिशा भी है, इसे केवल एक अदिश मान का उपयोग करके खोजना असंभव है। लेकिन इसके अलावा, निर्देशांक का उपयोग करके हमें दिए गए वैक्टर को खोजने का एक और तरीका है।
हमें वैक्टर $\overline(α)$ और $\overline(β)$ दिए जाएं, जिसमें क्रमशः $(α_1,α_2,α_3)$ और $(β_1,β_2,β_3)$ निर्देशांक होंगे। फिर क्रॉस उत्पाद का वेक्टर (अर्थात्, इसके निर्देशांक) निम्न सूत्र द्वारा पाया जा सकता है:
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
अन्यथा, निर्धारक का विस्तार करते हुए, हम निम्नलिखित निर्देशांक प्राप्त करते हैं
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
उदाहरण 2
निर्देशांक $(0,3,3)$ और $(-1,2,6)$ के साथ कोलीनियर वैक्टर $\overline(α)$ और $\overline(β)$ के क्रॉस उत्पाद के वेक्टर का पता लगाएं।
समाधान.
आइए उपरोक्त सूत्र का उपयोग करें। पाना
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
उत्तर: $(12,-3,3)$।
मनमाने ढंग से मिश्रित तीन वैक्टर $\overline(α)$, $\overline(β)$ और $\overline(γ)$, साथ ही $r∈R$ के लिए, निम्नलिखित गुण हैं:
उदाहरण 3
उस समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ और $(3,8,0) हैं $।
समाधान.
सबसे पहले, इस समांतर चतुर्भुज को निर्देशांक स्थान में खींचें (चित्र 5):
चित्र 5. निर्देशांक स्थान में समांतर चतुर्भुज। लेखक24 - छात्र पत्रों का ऑनलाइन आदान-प्रदान
हम देखते हैं कि इस समांतर चतुर्भुज के दो पक्षों को निर्देशांक $\overline(α)=(3,0,0)$ और $\overline(β)=(0,8,0)$ के साथ कोलीनियर वैक्टर का उपयोग करके बनाया गया है। चौथी संपत्ति का उपयोग करते हुए, हम प्राप्त करते हैं:
$S=|\overline(α)x\overline(β)|$
वेक्टर खोजें $\overline(α)х\overline(β)$:
$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
इस तरह
$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$
इस पाठ में, हम सदिशों के साथ दो और संक्रियाओं को देखेंगे: वैक्टर का क्रॉस उत्पादऔर वैक्टर का मिश्रित उत्पाद (जिन्हें इसकी आवश्यकता है उनके लिए तत्काल लिंक). यह ठीक है, कभी-कभी ऐसा होता है कि पूर्ण सुख के लिए भी वैक्टर का डॉट उत्पादअधिक से अधिक की जरूरत है। ऐसी है वेक्टर एडिक्शन। किसी को यह आभास हो सकता है कि हम विश्लेषणात्मक ज्यामिति के जंगल में जा रहे हैं। यह गलत है। उच्च गणित के इस खंड में आमतौर पर बहुत कम जलाऊ लकड़ी होती है, सिवाय शायद पिनोचियो के लिए। वास्तव में, सामग्री बहुत ही सामान्य और सरल है - शायद ही उससे अधिक कठिन हो अदिश उत्पाद, यहां तक कि कम विशिष्ट कार्य भी होंगे। विश्लेषणात्मक ज्यामिति में मुख्य बात, जैसा कि बहुत से लोग देखेंगे या पहले ही देख चुके हैं, गलत गणना नहीं है। एक जादू की तरह दोहराएं, और आप खुश होंगे =)
यदि वेक्टर कहीं दूर चमकते हैं, जैसे क्षितिज पर बिजली, इससे कोई फर्क नहीं पड़ता, पाठ से शुरू करें डमी के लिए वैक्टरवैक्टर के बारे में बुनियादी ज्ञान को पुनर्स्थापित करने या पुनः प्राप्त करने के लिए। अधिक तैयार पाठक चुनिंदा जानकारी से परिचित हो सकते हैं, मैंने व्यावहारिक कार्यों में अक्सर पाए जाने वाले उदाहरणों का सबसे पूरा संग्रह एकत्र करने की कोशिश की
आपको क्या खुश करेगा? जब मैं छोटा था, तो मैं दो या तीन गेंदों को भी हथकंडा दे सकता था। इसने अच्छा काम किया। अब हथकंडा करने की बिल्कुल जरूरत नहीं है, क्योंकि हम विचार करेंगे केवल अंतरिक्ष वैक्टर, और दो निर्देशांक वाले समतल सदिशों को छोड़ दिया जाएगा। क्यों? इस प्रकार इन क्रियाओं का जन्म हुआ - वैक्टर के वेक्टर और मिश्रित उत्पाद परिभाषित होते हैं और त्रि-आयामी अंतरिक्ष में काम करते हैं। पहले से आसान!
इस ऑपरेशन में, उसी तरह जैसे स्केलर उत्पाद में, दो वैक्टर. इसे अविनाशी अक्षर होने दो।
कार्रवाई ही लक्षितइस अनुसार: । अन्य विकल्प भी हैं, लेकिन मैं इस तरह से वैक्टर के क्रॉस उत्पाद को एक क्रॉस के साथ वर्ग कोष्ठक में नामित करने के लिए उपयोग किया जाता हूं।
और तुरंत सवाल: मैं फ़िन वैक्टर का डॉट उत्पाददो वैक्टर शामिल हैं, और यहां दो वैक्टर भी गुणा किए जाते हैं क्या अंतर है? एक स्पष्ट अंतर, सबसे पहले, परिणाम में:
सदिशों के अदिश गुणनफल का परिणाम एक NUMBER है:
वैक्टर के क्रॉस उत्पाद का नतीजा एक वेक्टर है: अर्थात, हम सदिशों को गुणा करते हैं और पुन: सदिश प्राप्त करते हैं। बंद क्लब। दरअसल, इसलिए ऑपरेशन का नाम। विभिन्न शैक्षिक साहित्य में, पदनाम भी भिन्न हो सकते हैं, मैं पत्र का उपयोग करूंगा।
पहले चित्र के साथ परिभाषा होगी, फिर टिप्पणियाँ होंगी।
परिभाषा: पार उत्पाद गैर समरेखवैक्टर, इस क्रम में लिया, वेक्टर कहा जाता है, लंबाईजो संख्यात्मक रूप से है समांतर चतुर्भुज के क्षेत्रफल के बराबर, इन सदिशों पर निर्मित; वेक्टर वैक्टर के लिए ऑर्थोगोनल, और निर्देशित किया जाता है ताकि आधार का सही अभिविन्यास हो:
हम हड्डियों द्वारा परिभाषा का विश्लेषण करते हैं, बहुत सारी दिलचस्प बातें हैं!
तो, हम निम्नलिखित महत्वपूर्ण बिंदुओं को उजागर कर सकते हैं:
1) स्रोत सदिश , परिभाषा के अनुसार, लाल तीरों द्वारा दर्शाया गया है संरेख नहीं. संरेख सदिशों के मामले पर थोड़ी देर बाद विचार करना उचित होगा।
2) वैक्टर लिए गए सख्त क्रम में: – "ए" को "बी" से गुणा किया जाता है, "हो" से "ए" नहीं। सदिश गुणन का परिणाम VECTOR है, जिसे नीले रंग से दर्शाया गया है। यदि सदिशों को उल्टे क्रम में गुणा किया जाता है, तो हमें लम्बाई में बराबर और दिशा में विपरीत (लाल रंग) सदिश मिलता है। यानी समता 
.
3) आइए अब सदिश गुणनफल के ज्यामितीय अर्थ से परिचित हों। यह एक बहुत महत्वपूर्ण मुद्दा है! नीले वेक्टर की लंबाई (और, इसलिए, क्रिमसन वेक्टर) संख्यात्मक रूप से वैक्टर पर बने समांतर चतुर्भुज के क्षेत्रफल के बराबर है। चित्र में, इस समांतर चतुर्भुज को काले रंग से छायांकित किया गया है।
टिप्पणी : ड्राइंग योजनाबद्ध है, और निश्चित रूप से, क्रॉस उत्पाद की नाममात्र लंबाई समानांतर चतुर्भुज के क्षेत्र के बराबर नहीं है।
हम ज्यामितीय सूत्रों में से एक को याद करते हैं: एक समांतर चतुर्भुज का क्षेत्रफल आसन्न भुजाओं के गुणनफल और उनके बीच के कोण की ज्या के बराबर होता है. इसलिए, पूर्वगामी के आधार पर, वेक्टर उत्पाद की लंबाई की गणना करने का सूत्र मान्य है:
मैं इस बात पर जोर देता हूं कि सूत्र में हम वेक्टर की लंबाई के बारे में बात कर रहे हैं, न कि वेक्टर के बारे में। व्यावहारिक अर्थ क्या है? और अर्थ ऐसा है कि विश्लेषणात्मक ज्यामिति की समस्याओं में, एक समांतर चतुर्भुज का क्षेत्र अक्सर एक सदिश उत्पाद की अवधारणा के माध्यम से पाया जाता है:
हमें दूसरा महत्वपूर्ण सूत्र मिलता है। समांतर चतुर्भुज (लाल बिंदीदार रेखा) का विकर्ण इसे दो समान त्रिभुजों में विभाजित करता है। इसलिए, वैक्टर (लाल छायांकन) पर निर्मित त्रिभुज का क्षेत्रफल सूत्र द्वारा पाया जा सकता है:
4) एक समान रूप से महत्वपूर्ण तथ्य यह है कि सदिश सदिशों के लिए ओर्थोगोनल है, अर्थात 
. बेशक, विपरीत रूप से निर्देशित वेक्टर (क्रिमसन एरो) भी मूल वैक्टर के लिए ऑर्थोगोनल है।
5) वेक्टर को निर्देशित किया जाता है ताकि आधारयह है सहीअभिविन्यास। के बारे में एक पाठ में एक नए आधार पर संक्रमणके बारे में विस्तार से बता चुका हूं विमान अभिविन्यास, और अब हम यह पता लगाएंगे कि अंतरिक्ष का अभिविन्यास क्या है। मैं आपकी उंगलियों पर समझाऊंगा दांया हाथ. मानसिक रूप से गठबंधन करें तर्जनी अंगुलीवेक्टर के साथ और बीच की ऊँगलीवेक्टर के साथ। अनामिका और कनिष्ठिकाअपनी हथेली में दबाएं। नतीजतन अँगूठा- वेक्टर उत्पाद दिखेगा। यह सही-उन्मुख आधार है (यह चित्र में है)। अब सदिशों की अदला-बदली करें ( तर्जनी और मध्यमा) कुछ स्थानों पर, अंगूठा घूम जाएगा, और वेक्टर उत्पाद पहले से ही नीचे दिखेगा। यह भी एक दक्षिणपंथी आधार है। शायद आपके पास एक प्रश्न है: वामपंथी अभिविन्यास किस आधार पर है? "असाइन करें" एक ही उंगलियां बायां हाथ vectors , और बायाँ आधार और बायाँ स्थान अभिविन्यास प्राप्त करें (इस स्थिति में, अंगूठा निचले सदिश की दिशा में स्थित होगा). आलंकारिक रूप से बोलते हुए, ये आधार अलग-अलग दिशाओं में "मोड़" या उन्मुख स्थान हैं। और इस अवधारणा को कुछ दूर की कौड़ी या अमूर्त नहीं माना जाना चाहिए - उदाहरण के लिए, सबसे साधारण दर्पण अंतरिक्ष के उन्मुखीकरण को बदलता है, और यदि आप "प्रतिबिंबित वस्तु को दर्पण से बाहर खींचते हैं", तो सामान्य तौर पर यह संभव नहीं होगा इसे "मूल" के साथ मिलाएं। वैसे, तीन अंगुलियों को दर्पण में लाएं और प्रतिबिंब का विश्लेषण करें ;-)
... यह कितना अच्छा है कि अब आप इसके बारे में जान गए हैं दाएं और बाएं उन्मुखआधार, क्योंकि अभिविन्यास परिवर्तन के बारे में कुछ व्याख्याताओं के बयान भयानक हैं =)
परिभाषा पर विस्तार से काम किया गया है, यह पता लगाना बाकी है कि जब वैक्टर संरेख होते हैं तो क्या होता है। यदि सदिश समतल हैं, तो उन्हें एक सीधी रेखा पर रखा जा सकता है और हमारा समांतर चतुर्भुज भी एक सीधी रेखा में "गुना" होता है। ऐसा क्षेत्र, जैसा कि गणितज्ञ कहते हैं, पतितसमानांतर चतुर्भुज शून्य है। सूत्र से भी यही होता है - शून्य या 180 डिग्री की ज्या शून्य के बराबर होती है, जिसका अर्थ है कि क्षेत्रफल शून्य है
इस प्रकार, यदि, तब 
और 
. कृपया ध्यान दें कि क्रॉस उत्पाद स्वयं शून्य वेक्टर के बराबर है, लेकिन व्यवहार में इसे अक्सर उपेक्षित किया जाता है और लिखा जाता है कि यह भी शून्य के बराबर है।
एक विशेष मामला वेक्टर और स्वयं का वेक्टर उत्पाद है:
क्रॉस उत्पाद का उपयोग करके, आप त्रि-आयामी वैक्टर की संपार्श्विकता की जांच कर सकते हैं, और हम इस समस्या का विश्लेषण भी करेंगे।
व्यावहारिक उदाहरणों को हल करने के लिए यह आवश्यक हो सकता है त्रिकोणमितीय तालिकाइससे ज्या के मूल्यों का पता लगाने के लिए।
खैर, आग लगाओ:
उदाहरण 1
ए) वैक्टर के वेक्टर उत्पाद की लंबाई पाएं यदि 
ख) सदिशों पर निर्मित समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए यदि 
समाधान: नहीं, यह कोई टाइपो नहीं है, मैंने जानबूझकर प्रारंभिक डेटा को स्थिति में समान बनाया है। क्योंकि समाधानों का डिज़ाइन अलग होगा!
a) स्थिति के अनुसार, इसे खोजना आवश्यक है लंबाईवेक्टर (वेक्टर उत्पाद)। संबंधित सूत्र के अनुसार:
उत्तर:
चूंकि यह लंबाई के बारे में पूछा गया था, तो उत्तर में हम आयाम - इकाइयों का संकेत देते हैं।
b) स्थिति के अनुसार, इसे खोजना आवश्यक है वर्गवैक्टर पर निर्मित समांतर चतुर्भुज। इस समांतर चतुर्भुज का क्षेत्रफल संख्यात्मक रूप से क्रॉस उत्पाद की लंबाई के बराबर है:
उत्तर:
कृपया ध्यान दें कि वेक्टर उत्पाद के उत्तर में कोई बात नहीं है, जिसके बारे में हमसे पूछा गया था आंकड़ा क्षेत्र, क्रमशः, आयाम वर्ग इकाई है।
हम हमेशा देखते हैं कि स्थिति के अनुसार क्या खोजना आवश्यक है, और इसके आधार पर, हम तैयार करते हैं साफ़उत्तर। यह शाब्दिक प्रतीत हो सकता है, लेकिन शिक्षकों के बीच पर्याप्त साहित्यकार हैं, और अच्छे अवसरों वाले कार्य को संशोधन के लिए वापस कर दिया जाएगा। यद्यपि यह विशेष रूप से तनावपूर्ण नाइटपिक नहीं है - यदि उत्तर गलत है, तो किसी को यह आभास हो जाता है कि व्यक्ति साधारण चीजों को नहीं समझता है और / या कार्य के सार को नहीं समझा है। उच्च गणित और अन्य विषयों में भी किसी भी समस्या को हल करते हुए इस क्षण को हमेशा नियंत्रण में रखना चाहिए।
बड़ा अक्षर "एन" कहाँ गया? सिद्धांत रूप में, यह अतिरिक्त रूप से समाधान के लिए अटका हो सकता है, लेकिन रिकॉर्ड को छोटा करने के लिए, मैंने नहीं किया। मुझे आशा है कि हर कोई इसे समझता है और एक ही चीज़ का पदनाम है।
डू-इट-खुद समाधान के लिए एक लोकप्रिय उदाहरण:
उदाहरण 2
यदि सदिशों पर बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए 
वेक्टर उत्पाद के माध्यम से त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र टिप्पणियों में परिभाषा में दिया गया है। पाठ के अंत में समाधान और उत्तर।
व्यवहार में, कार्य वास्तव में बहुत सामान्य है, त्रिभुजों को आमतौर पर प्रताड़ित किया जा सकता है।
अन्य समस्याओं को हल करने के लिए, हमें चाहिए:
हमने वेक्टर उत्पाद के कुछ गुणों पर पहले ही विचार कर लिया है, हालाँकि, मैं उन्हें इस सूची में शामिल करूँगा।
मनमाना वैक्टर और मनमाना संख्या के लिए, निम्नलिखित गुण सत्य हैं:
1) जानकारी के अन्य स्रोतों में, यह आइटम आमतौर पर गुणों में प्रतिष्ठित नहीं है, लेकिन यह व्यावहारिक रूप से बहुत महत्वपूर्ण है। तो रहने दो।
2) 
- संपत्ति की भी चर्चा ऊपर की गई है, कभी-कभी इसे कहा जाता है anticommutativity. दूसरे शब्दों में, सदिशों का क्रम मायने रखता है।
3) - संयोजन या जोड़नेवालावेक्टर उत्पाद कानून। सदिश उत्पाद की सीमा से स्थिरांक आसानी से निकाल लिए जाते हैं। वास्तव में, वे वहाँ क्या कर रहे हैं?
4) - वितरण या वितरणवेक्टर उत्पाद कानून। कोष्ठक खोलने में भी कोई समस्या नहीं है।
एक प्रदर्शन के रूप में, एक संक्षिप्त उदाहरण पर विचार करें:
उदाहरण 3
अगर खोजो 
समाधान:शर्त के अनुसार, सदिश उत्पाद की लंबाई का पता लगाना फिर से आवश्यक है। आइए हमारे लघुचित्र को पेंट करें: 
(1) साहचर्य कानूनों के अनुसार, हम वेक्टर उत्पाद की सीमा से परे स्थिरांक निकालते हैं।
(2) हम मॉड्यूल से स्थिरांक निकालते हैं, जबकि मॉड्यूल माइनस साइन को "खा" देता है। लंबाई ऋणात्मक नहीं हो सकती।
(3) जो आगे है वह स्पष्ट है।
उत्तर: 
आग पर लकड़ी फेंकने का समय आ गया है:
उदाहरण 4
सदिशों पर निर्मित त्रिभुज के क्षेत्रफल की गणना करें यदि 
समाधान: सूत्र की सहायता से त्रिभुज का क्षेत्रफल ज्ञात कीजिए 
. रोड़ा यह है कि वैक्टर "सीई" और "टी" स्वयं वैक्टर के योग के रूप में दर्शाए जाते हैं। यहाँ एल्गोरिथ्म मानक है और कुछ हद तक पाठ के उदाहरण संख्या 3 और 4 की याद दिलाता है। वैक्टर का डॉट उत्पाद. आइए इसे स्पष्टता के लिए तीन चरणों में विभाजित करें:
1) पहले चरण में, हम वेक्टर उत्पाद को वेक्टर उत्पाद के माध्यम से व्यक्त करते हैं, वास्तव में, वेक्टर को वेक्टर के संदर्भ में व्यक्त करें. लंबाई पर अभी तक कोई शब्द नहीं!
(1) हम सदिशों के व्यंजकों को प्रतिस्थापित करते हैं।
(2) वितरण के नियमों का उपयोग करते हुए, हम बहुपदों के गुणन के नियम के अनुसार कोष्ठक खोलते हैं।
(3) साहचर्य कानूनों का उपयोग करते हुए, हम वेक्टर उत्पादों से परे सभी स्थिरांक निकालते हैं। थोड़े से अनुभव के साथ, क्रियाएं 2 और 3 एक साथ की जा सकती हैं।
(4) सुखद संपत्ति के कारण पहला और अंतिम पद शून्य (शून्य वेक्टर) के बराबर है। दूसरे कार्यकाल में, हम सदिश उत्पाद के एंटीकॉम्यूटिविटी गुण का उपयोग करते हैं:
(5) हम समान शब्द प्रस्तुत करते हैं।
नतीजतन, वेक्टर एक वेक्टर के माध्यम से व्यक्त किया गया, जिसे प्राप्त करने की आवश्यकता थी: 
2) दूसरे चरण में, हमें आवश्यक वेक्टर उत्पाद की लंबाई का पता चलता है। यह क्रिया उदाहरण 3 के समान है: 
3) वांछित त्रिभुज का क्षेत्रफल ज्ञात कीजिए: 
समाधान के चरण 2-3 को एक पंक्ति में व्यवस्थित किया जा सकता है।
उत्तर:
माना समस्या परीक्षणों में काफी आम है, यहाँ एक स्वतंत्र समाधान के लिए एक उदाहरण है:
उदाहरण 5
अगर खोजो
पाठ के अंत में संक्षिप्त समाधान और उत्तर। आइए देखें कि पिछले उदाहरणों का अध्ययन करते समय आप कितने चौकस थे ;-)
सूत्र वास्तव में सरल है: हम निर्धारक की शीर्ष पंक्ति में निर्देशांक वैक्टर लिखते हैं, हम दूसरी और तीसरी पंक्तियों में वैक्टर के निर्देशांक को "पैक" करते हैं, और हम डालते हैं सख्त क्रम में- पहले, वेक्टर "ve" के निर्देशांक, फिर वेक्टर "डबल-ve" के निर्देशांक। यदि वैक्टर को एक अलग क्रम में गुणा करने की आवश्यकता है, तो लाइनों की अदला-बदली भी की जानी चाहिए: 
उदाहरण 10
जांचें कि क्या निम्नलिखित अंतरिक्ष वैक्टर संरेख हैं:
ए)
बी) 
समाधान: परीक्षण इस पाठ में दिए गए कथनों में से एक पर आधारित है: यदि सदिश समरेख हैं, तो उनका क्रॉस उत्पाद शून्य (शून्य सदिश) है: 
.
ए) वेक्टर उत्पाद खोजें: 
इसलिए सदिश समरेख नहीं हैं।
बी) वेक्टर उत्पाद खोजें: 
उत्तर: ए) समरेख नहीं, बी)
यहाँ, शायद, सदिशों के सदिश गुणनफल के बारे में सभी बुनियादी जानकारी है।
यह खंड बहुत बड़ा नहीं होगा, क्योंकि कुछ समस्याएँ हैं जहाँ सदिशों के मिश्रित उत्पाद का उपयोग किया जाता है। वास्तव में, सब कुछ परिभाषा, ज्यामितीय अर्थ और कुछ कामकाजी सूत्रों पर आधारित होगा।
सदिशों का मिश्रित उत्पाद तीन सदिशों का गुणनफल होता है:
इस तरह वे एक ट्रेन की तरह खड़े होते हैं और प्रतीक्षा करते हैं, जब तक उनकी गणना नहीं हो जाती तब तक वे प्रतीक्षा नहीं कर सकते।
पहले फिर से परिभाषा और चित्र:
परिभाषा: मिश्रित उत्पाद गैर समतलीयवैक्टर, इस क्रम में लिया, कहा जाता है समांतर चतुर्भुज की मात्रा, इन सदिशों पर निर्मित, यदि आधार सही है तो "+" चिह्न और आधार छोड़े जाने पर "-" चिन्ह से सुसज्जित है।
चलो ड्राइंग करते हैं। हमारे लिए अदृश्य रेखाएँ बिंदीदार रेखा द्वारा खींची जाती हैं: 
आइए परिभाषा में गोता लगाएँ:
2) वैक्टर लिए गए एक निश्चित क्रम में, अर्थात्, उत्पाद में वैक्टर का क्रमचय, जैसा कि आप अनुमान लगा सकते हैं, परिणाम के बिना नहीं जाता है।
3) ज्यामितीय अर्थ पर टिप्पणी करने से पहले, मैं स्पष्ट तथ्य पर ध्यान दूंगा: सदिशों का मिश्रित गुणनफल एक NUMBER है: . शैक्षिक साहित्य में, डिजाइन कुछ अलग हो सकता है, मैं एक मिश्रित उत्पाद को नामित करता था, और "पे" अक्षर के साथ गणना का परिणाम।
ए-प्राथमिकता मिश्रित उत्पाद समांतर चतुर्भुज का आयतन है, वैक्टर पर निर्मित (आकृति लाल वैक्टर और काली रेखाओं के साथ खींची गई है)। अर्थात्, संख्या दिए गए समांतर चतुर्भुज के आयतन के बराबर है।
टिप्पणी : आरेखण योजनाबद्ध है।
4) आइए फिर से आधार और स्थान के उन्मुखीकरण की अवधारणा से परेशान न हों। अंतिम भाग का अर्थ यह है कि वॉल्यूम में माइनस साइन जोड़ा जा सकता है। सरल शब्दों में, मिश्रित उत्पाद ऋणात्मक हो सकता है: .
सदिशों पर बने समांतर चतुर्भुज के आयतन की गणना करने का सूत्र सीधे परिभाषा से अनुसरण करता है।
जाहिर है, एक क्रॉस उत्पाद के मामले में, जिस क्रम में वैक्टर लिया जाता है, इसके अलावा, मायने रखता है,
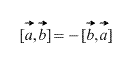
इसके अलावा, सीधे परिभाषा से यह इस प्रकार है कि किसी भी अदिश कारक k (संख्या) के लिए निम्नलिखित सत्य है:
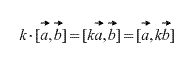
समरेख सदिशों का अनुप्रस्थ गुणनफल शून्य सदिश के बराबर होता है। इसके अलावा, दो सदिशों का क्रॉस उत्पाद शून्य है यदि और केवल यदि वे संरेख हैं। (यदि उनमें से एक शून्य सदिश है तो यह याद रखना आवश्यक है कि परिभाषा के अनुसार शून्य सदिश किसी भी सदिश के समरेख है)।
वेक्टर उत्पाद है वितरण की जाने वाली संपत्ति, वह है
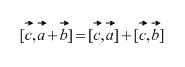
सदिशों के निर्देशांकों के संदर्भ में क्रॉस उत्पाद की अभिव्यक्ति।
मान लीजिए कि दो सदिश दिए गए हैं
(इसकी शुरुआत और अंत के निर्देशांक द्वारा एक वेक्टर के निर्देशांक कैसे खोजें - लेख देखें वैक्टर का डॉट उत्पाद, डॉट उत्पाद का पैराग्राफ वैकल्पिक परिभाषा, या उनके निर्देशांक द्वारा दिए गए दो वैक्टर के डॉट उत्पाद की गणना करना।)
आपको वेक्टर उत्पाद की आवश्यकता क्यों है?
क्रॉस उत्पाद का उपयोग करने के कई तरीके हैं, उदाहरण के लिए, जैसा कि पहले ही ऊपर लिखा गया है, दो वैक्टरों के क्रॉस उत्पाद की गणना करके, आप यह पता लगा सकते हैं कि क्या वे संरेख हैं।
या इसका उपयोग इन वैक्टरों से निर्मित समांतर चतुर्भुज के क्षेत्रफल की गणना करने के तरीके के रूप में किया जा सकता है। परिभाषा के आधार पर, परिणामी सदिश की लंबाई इस समांतर चतुर्भुज का क्षेत्रफल है।
साथ ही, बिजली और चुंबकत्व में बड़ी संख्या में अनुप्रयोग मौजूद हैं।वेक्टर उत्पाद का ऑनलाइन कैलकुलेटर।
इस कैलकुलेटर का उपयोग करके दो वैक्टरों के स्केलर उत्पाद को खोजने के लिए, आपको पहली पंक्ति में पहली पंक्ति में पहले वेक्टर के निर्देशांक दर्ज करने होंगे, और दूसरे में दूसरे वेक्टर को दर्ज करना होगा। वैक्टर के निर्देशांक की गणना उनके प्रारंभ और अंत निर्देशांक से की जा सकती है (लेख देखें वैक्टर का डॉट उत्पाद, आइटम डॉट उत्पाद की एक वैकल्पिक परिभाषा, या उनके निर्देशांक दिए गए दो वैक्टरों के डॉट उत्पाद की गणना करना।)
